In [1]:
import sys
sys.path.append("../")
from common import utils
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
6 グラフの行列表現とその固有値、固有ベクトル¶
- グラフを行列で表し、行列の特徴からグラフの特徴を理解します。
6.1 隣接行列¶
- 行、列を単語として、それらが隣接していれば1、隣接していなければ0となるような行列を隣接行列と呼びます。
- 以下は、"A boy crimbed every tree."の依存関係を行列で表現したものです。
- この行列の列の和はその単語の次数になります。
| 1 A | 2 boy | 3 climbed | 4 every | 5 tree | 6 . | |
|---|---|---|---|---|---|---|
| 1 A | 0 | 1 | 0 | 0 | 0 | 0 |
| 2 boy | 1 | 0 | 1 | 0 | 0 | 0 |
| 3 climbed | 0 | 1 | 0 | 0 | 1 | 1 |
| 4 every | 0 | 0 | 0 | 0 | 1 | 0 |
| 5 tree | 0 | 0 | 1 | 1 | 0 | 0 |
| 6 . | 0 | 0 | 1 | 0 | 0 | 0 |
演習問題8¶
spaCyを用いて"A boy climbed every tree."の依存関係を抽出し、この依存関係を隣接行列で表現してみましょう。
6.2 次数行列¶
- 行列の対角成分にその単語次数を示した行列を次数行列と呼びます。
- 以下は、"A boy climbed every tree."の次数行列です。
| 1 A | 2 boy | 3 climbed | 4 every | 5 tree | 6 . | |
|---|---|---|---|---|---|---|
| 1 A | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 boy | 0 | 2 | 0 | 0 | 0 | 0 |
| 3 climbed | 0 | 0 | 3 | 0 | 0 | 0 |
| 4 every | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 tree | 0 | 0 | 0 | 0 | 2 | 0 |
| 6 . | 0 | 0 | 0 | 0 | 0 | 1 |
演習問題9¶
演習問題9で算出した隣接行列を用いて"A boy climbed every tree."を次数行列で表現してみましょう。
6.3 グラフラプラシアン¶
次数行列から隣接行列を引いた行列をグラフラプラシアンと言います。
演習問題10¶
"A boy climbed every tree."のグラフラプラシアンを求めましょう。
6.4 グラフラプラシアンの固有値と固有ベクトル¶
- 木から求められるグラフラプラシアンは木の特徴を表しています。
- スペクトル半径(最大の固有値): 根が持つエッジの数(木の平坦さ)
- 代数的連結(2番目に小さい固有値): 木の深さ
- 固有ベクトル中心性(最大の固有値に属する固有ベクトル): 個々のノードの中心性
- フィードラーベクトル(2番目に小さい固有値に属する固有ベクトル): ノード同士のまとまり
- 固有値の合計は辺の数の2倍
- 最大の固有値とその固有値に属する固有ベクトルは以下のように求めます。
In [2]:
M1 = np.array([[1,2,0],[2,1,1],[1,0,1]])
M1
Out[2]:
array([[1, 2, 0],
[2, 1, 1],
[1, 0, 1]])
In [3]:
E,v = np.linalg.eig(M1)
E
Out[3]:
array([ 3.21431974, -0.67513087, 0.46081113])
In [4]:
v
Out[4]:
array([[ 0.64153318, 0.69709062, -0.47075835],
[ 0.71027979, -0.58385901, 0.12691383],
[ 0.28972021, -0.41614099, 0.87308617]])
In [5]:
v.T[0]
Out[5]:
array([0.64153318, 0.71027979, 0.28972021])
演習問題11¶
以下の文の依存木のグラフラプラシアンの固有値を求めてみましょう(ピリオドは除いて解析してます)。
She became a teacher after she graduated from some univeristy
演習問題13¶
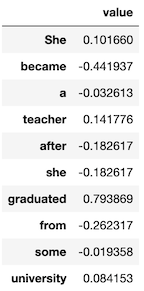
上の文のフィードラーベクトルを求め、以下のように表示してみましょう。
- 最大の固有値に属するベクトルはノードのまとまりを示しています。
- 以下のように図示することによってノードのまとまりが可視化されます。
- 以下のリンクから自作関数の利用方法に関する説明が読めます。
In [6]:
text = "She became a teacher after she graduated from some univeristy"
V,E = utils.text_to_set_i(text)
G_adj,G_deg,G_lap = utils.set_to_M(V,E)
E,v = np.linalg.eig(G_lap)
E = [np.abs(i) for i in E]
D1 = {}
for i,j in zip(E,v.T):
D1[i] = j
D1x = sorted(D1.items())
words = text.split()
df1 = pd.DataFrame({"value":D1x[-1][1]},index = words)
plt.figure(figsize=(20, 4),dpi=350)
X = list(range(len(text.split())))
plt.xticks(X,text.split())
for i,j in zip(X,df1["value"]):
plt.scatter(i,j.real,color="k",s=80)
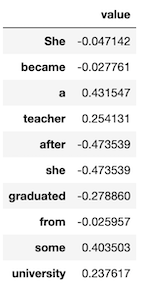
- フィードラーベクトルも同様に図示します。
In [7]:
df2 = pd.DataFrame({"value":D1x[2][1]},index = words)
plt.figure(figsize=(20, 4),dpi=350)
X = list(range(len(text.split())))
plt.xticks(X,text.split())
for i,j in zip(X,df2["value"]):
plt.scatter(i,j.real,color="k",s=80)
- 理解のために、これらを依存木に表してみます。
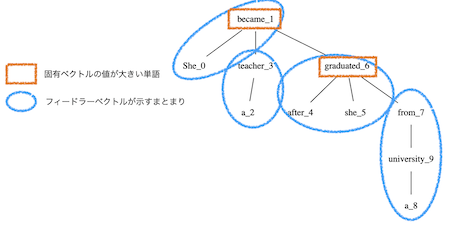
演習問題14¶
../DATA01/sentences.txtの各文において、木の深さ、木の平坦さ、スペクトル半径(最大の固有値)、代数的連結(2番目に小さい固有値)を求めてみましょう。また、木の深さと代数的連結、スペクトル半径と木の平坦さの散布図を描いてみましょう。