学習者言語の分析（応用）2（第3回）

  • 5 行列
    • 5.1 行列に関する名称
    • 5.2 行列の演算
      • 和と差
      • スカラー倍
      • 積
    • 5.3 単位行列
    • 5.4 逆行列
    • 5.5 Numpyで行列を扱う
      • 行列の生成
      • 行列の成分の取得と代入
      • 行列の演算
    • 5.6 固有値
      • 行列による線形変換
      • 固有値・固有ベクトル
    • 5.7 固有値の解釈

5 行列¶

5.1 行列に関する名称¶

  • 以下のように数が縦、横に並んだものを行列と言う。

$$ \left( \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right) $$

  • この行列の横を行、縦を列と言う。

    • 1行目には1と2があり、
    • 1列目には1と3がある。

  • それぞれの数のことを成分と言う。

    • この行列の2行1列の成分は3である。

  • 行と列の数を加えて、$n \times m$行列と言うことがある。

    • 上の行列は$2 \times 2 $行列である。

  • 上の行列のように行数と列数が同じものを正方行列と言う。

  • 行列は「行列$A$」のように大文字で、成分は小文字で表される。

$$ A = \left( \begin{matrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{matrix} \right) $$

5.2 行列の演算¶

  • 行列の和は対応する成分同士の和である。

和と差¶

$$ \left( \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right) + \left( \begin{matrix} 5 & 6 \\ 7 & 8 \end{matrix} \right) = \left( \begin{matrix} 1 + 5 & 2 + 6 \\ 3+7 & 4 + 8 \end{matrix} \right) = \left( \begin{matrix} 6 & 8 \\ 10 & 12 \end{matrix} \right) $$

  • 行列の差も同様である。
  • そのため、行数、列数が異なる行列同士の和と差は定義されない。

スカラー倍¶

  • 以下のように定義される。

$$ 4 \times \left( \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right) = \left( \begin{matrix} 4 \times 1 & 4 \times 2\\ 4 \times 3& 4 \times 4 \end{matrix} \right) = \left( \begin{matrix} 4 & 8 \\ 12& 16 \end{matrix} \right) $$

積¶

  • ２つの行列$A$、$B$がある時、これらの行列の積は$AB$と表される。
  • 行列$A$の列数と行列$B$の行数が同じである時のみ積$AB$が定義される。
  • 積$AB$の$i$行目$j$列目の成分は、行列$A$の$i$行の成分と行列$B$の$j$列の成分を順にかけたものの総和である。

$$ \left( \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right) \times \left( \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix} \right) = \left( \begin{matrix} 1 \times 1 + 2 \times 4 & 1 \times 2 + 2 \times 5 & 1 \times 3 + 2 \times 6 \\ 1 \times 3 + 4 \times 4 & 2 \times 3 + 4 \times 5 & 3 \times 3 + 4 \times 6 \end{matrix} \right) = \left( \begin{matrix} 9 & 13 & 15 \\ 19 & 26 & 33 \end{matrix} \right) $$

  • $AB$の積が求められても、$BA$が定義できない場合もあれば、結果が異なる場合もある。

5.3 単位行列¶

  • 以下のように、行列の対角成分がすべて1で、それ以外の成分が0の行列を単位行列といい、${\it I}$で表す。

$$ \left( \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right) $$

  • 対角成分とは行列の左上からから右下へ向かう斜めの線上にある成分のことである。

  • 任意の行列に単位行列をかけてもその行列は変わらない。

$$ \left( \begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix} \right) \times \left( \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right) = \left( \begin{matrix} 1 & 2 \\ 3 & 4 \end{matrix} \right) $$

5.4 逆行列¶

  • 正方行列$A$に対し、以下が成立するような正方行列$A^{-1}$が存在する時、$A^{-1}$を$A$の逆行列と言う。

$$AA^{-1} = A^{-1}A = {\it I}$$

5.5 Numpyで行列を扱う¶

行列の生成¶

  • np.array()で生成する。
In [1]:
import numpy as np
In [2]:
M1 = np.array([[0,1,2],[4,5,6],[7,8,9]])
M1
Out[2]:
array([[0, 1, 2],
       [4, 5, 6],
       [7, 8, 9]])
In [3]:
# 成分がすべて0の３行3列の行列
M2 = np.zeros((3,3))
M2
Out[3]:
array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])
In [4]:
# 行数と列数の取得
M2.shape
Out[4]:
(3, 3)

行列の成分の取得と代入¶

In [5]:
# 行列M1の1行1列成分
M1[0][0]
Out[5]:
0
In [6]:
# 行列M2の2行2列目の成分に10を代入
M2[1][1] = 10

# 行列M2の1行3列目の成分に10を代入
M2[0][2] = 10

M2
Out[6]:
array([[ 0.,  0., 10.],
       [ 0., 10.,  0.],
       [ 0.,  0.,  0.]])

行列の演算¶

In [7]:
# M1 + M2
M1 + M2
Out[7]:
array([[ 0.,  1., 12.],
       [ 4., 15.,  6.],
       [ 7.,  8.,  9.]])
In [8]:
# 積
M1 @ M2
Out[8]:
array([[ 0., 10.,  0.],
       [ 0., 50., 40.],
       [ 0., 80., 70.]])
In [9]:
np.dot(M1,M2)
Out[9]:
array([[ 0., 10.,  0.],
       [ 0., 50., 40.],
       [ 0., 80., 70.]])
In [10]:
M1.dot(M2)
Out[10]:
array([[ 0., 10.,  0.],
       [ 0., 50., 40.],
       [ 0., 80., 70.]])
In [11]:
# 逆行列
M3 = np.array([[1,2],[5,6]])
M4 = np.linalg.inv(M3)
M4
Out[11]:
array([[-1.5 ,  0.5 ],
       [ 1.25, -0.25]])
In [12]:
M3 @ M4
Out[12]:
array([[1., 0.],
       [0., 1.]])
In [13]:
# すべての要素の合計値
np.sum(M3)
Out[13]:
14
In [14]:
# 列の合計値
np.sum(M3,axis=0)
Out[14]:
array([6, 8])
In [15]:
# 行の合計値
np.sum(M3,axis=1)
Out[15]:
array([ 3, 11])

5.6 固有値¶

行列による線形変換¶

  • 行列$A$とベクトル$x$の積$Ax$は以下のようになります。

$$ A = \left( \begin{matrix} 1 & 0 \\ -1 & 1 \end{matrix} \right) $$

$$ x = \left( \begin{matrix} x_1 \\ x_2 \end{matrix} \right) $$

$$ \left( \begin{matrix} 1 & 0 \\ -1 & 1 \end{matrix} \right) \left( \begin{matrix} x_1 \\ x_2 \end{matrix} \right) = \left( \begin{matrix} 1 \times x_1 + 0 \times x_2\\ -1 \times x_1 + 1\times x_2 \end{matrix} \right) $$

$$ = \left( \begin{matrix} x_1\\ -x_1 + x_2 \end{matrix} \right) $$

  • $x = (1,1)$とすると

$$ \left( \begin{matrix} 1 & 0 \\ -1 & 1 \end{matrix} \right) \left( \begin{matrix} 1 \\ 1 \end{matrix} \right) = \left( \begin{matrix} 1 \\ 0 \end{matrix} \right) $$

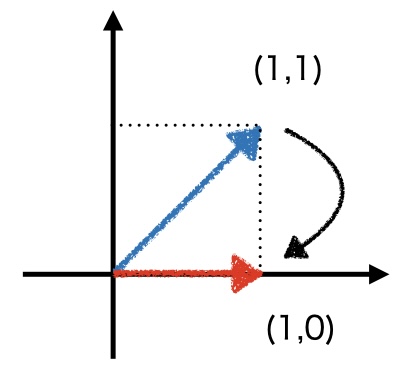
  • $x = (1,1)$に$A$をかけると$(1,0)$になりました。これを視覚的に表現すると以下のようになります。
  • つまり、ベクトルに行列をかけるという操作は「ベクトルを回転・伸縮させる」と捉えることもできます。 graph12

固有値・固有ベクトル¶

  • $ x \ne 0$のとき、行列$A$をかけると長さが$\lambda$倍になる$x$を固有ベクトル、$\lambda$を固有値と言います。 $$ Ax = \lambda x$$

  • つまり、固有ベクトルは行列$A$をかけても回転はせず、伸縮のみが施されるベクトルです。

  • NumPyでは以下のように求めます。

In [16]:
M = np.array([[4,-1],[2,1]])
E,V = np.linalg.eig(M)
print("固有値")
print(E)
print("固有ベクトル")
print(V)

固有値
[3. 2.]
固有ベクトル
[[0.70710678 0.4472136 ]
 [0.70710678 0.89442719]]
  • $ Ax = \lambda x$となっているか確認してみよう。
  • NumPyの出力ではベクトルが列になっているので注意。
In [17]:
M @ V.T[0]
Out[17]:
array([2.12132034, 2.12132034])
In [18]:
M @ V.T[1]
Out[18]:
array([0.89442719, 1.78885438])
  • 固有値3に対応する固有ベクトル(0.70710678, 0.70710678)に行列Mを施すと値が3倍になります(2.12132034, 2.12132034)。
  • 固有値2に対応する固有ベクトル(0.4472136 , 0.89442719)に行列Mを施すと値が2倍になります(0.89442719, 1.78885438)。

5.7 固有値の解釈¶

  • 人間の集団において、個人間の関係の強さを0から1までの値で表現します。
  • 対角成分は自分と自分の関係なので、とりあえず、0とします。
  • この行列の固有値を求めます。
In [19]:
import pandas as pd

M_1 = np.array([[0,0.2,0.2],[0.2,0,0.2],[0.2,0.2,0]])

Person3 = ["A","B","C"]

df1 = pd.DataFrame(M_1,columns = Person3,index=Person3)
df1
Out[19]:
A B C
A 0.0 0.2 0.2
B 0.2 0.0 0.2
C 0.2 0.2 0.0
In [20]:
E,v = np.linalg.eig(M_1)
E
Out[20]:
array([-0.2,  0.4, -0.2])
  • 次に、個人間の関係が強い集団の固有値を求めます。
In [21]:
M_2 = np.array([[0,0.8,0.8],[0.8,0,0.8],[0.8,0.8,0]])

df2 = pd.DataFrame(M_2,columns = Person3,index=Person3)
df2
Out[21]:
A B C
A 0.0 0.8 0.8
B 0.8 0.0 0.8
C 0.8 0.8 0.0
In [22]:
E,v = np.linalg.eig(M_2)
E
Out[22]:
array([-0.8,  1.6, -0.8])
  • 個人間の関係が強くなると最大の固有値の値が大きくなります。
  • 最後に、集団の中に関係が強い個人とそうでない個人が混在する場合での固有値を求めます（A, B, F間の関係、C, D, E間の関係が強く、その他の関係は弱い）。
In [23]:
M_3 = np.array([[0,0.9,0.1,0.1,0.1,0.8],[0.9,0,0.1,0.1,0.1,0.8],[0.1,0.1,0,0.9,0.9,0.1],[0.1,0.1,0.9,0,0.9,0.1],[0.1,0.1,0.9,0.9,0,0.2],[0.8,0.8,0.1,0.1,0.2,0]])

Person5 = ["A","B","C","D","E","F"]

df3 = pd.DataFrame(M_3,columns = Person5,index=Person5)
df3
Out[23]:
A B C D E F
A 0.0 0.9 0.1 0.1 0.1 0.8
B 0.9 0.0 0.1 0.1 0.1 0.8
C 0.1 0.1 0.0 0.9 0.9 0.1
D 0.1 0.1 0.9 0.0 0.9 0.1
E 0.1 0.1 0.9 0.9 0.0 0.2
F 0.8 0.8 0.1 0.1 0.2 0.0
In [24]:
E,V = np.linalg.eig(M_3)
E
Out[24]:
array([ 2.07358687,  1.39594997, -0.74020474, -0.9       , -0.92933209,
       -0.9       ])
  • 値が大きい固有値が2あります。
  • この人間関係表では、A, B, FのグループとC, D, Eのグループの２つのグループがある。
  • 固有値が集団全体の特性を表している可能性があります。