学習者言語の分析(応用)2(第2回)¶
4 木の特徴量¶
4.1 中心性¶
4.1.1 次数中心性¶
- 以下のグラフのノード1の次数は1で、ノード3の次数は4です。
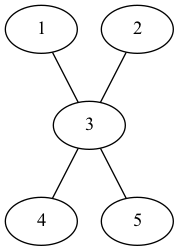
図1
- 中心性とは、グラフにおける各ノードの重要度を示す特徴量です。
- 最も簡単な特徴量は次数です。
- 単純グラフでは、次数の最大値は$n - 1$($n$はグラフ全体のノードの数)なので、次数を$n - 1$で割った正規化した値を用います。
- これを次数中心性(degree centrality)と呼びます。
|ノード番号|計算|次数中心性 |-----|-----|-----| |1|1/(5-1)| 0.25| |2|1/(5-1)| 0.25| |3|4/(5-1)| 1| |4|1/(5-1)| 0.25| |5|1/(5-1)| 0.25|
- 図からも明らかなように、ノード3が最も重要なノードということになります。
- ここで、「多くのノードと結ばれているノードは重要なノードである」という前提があります。
4.1.2 グラフ中心性 (Graph centrality)¶
- この次数中心性の考え方を利用してグラフ自体の構造の「深さ」に関する特徴量を算出することができます。
- 図1と図2のノードおよびエッジの数は同じだが、その構造は異なります。
- ここで、図1のグラフを最も「平らな」グラフ、図2のグラフを「深い」グラフと呼ぶことにします。
 図1(再掲)
図1(再掲)
 図2
図2
- この違いを表す特徴量を以下のように定義する。
$$ GC = \frac{\sum_{i=1}^{n}[C_x(p*) - C_x(p_i)]}{max\sum_{i=1}^{n}[C_x(p*) - C_x(p_i)]}$$
$C_x(p_i)$ : ノードの次数
$C_x(p*)$ : 当該グラフ上の$C_x(p_i)$の最大値
分母は与えられたノード数を持つグラフにおける最大値
式の解釈としては、与えられたノード数の場合の差の最大値と実際の値の比と考えられる。
図1と図2のGCを計算してみよう(ちなみに、分母は$n^2 - 3 n + 2$($n$はノード数)で求められる)
図1の場合
$$ GC_1 = \frac{(4 - 1) + (4 - 1) + (4 - 4) + (4 - 1) + (4 - 1)}{4^2 - 3 \times 4 + 2} $$
$$ = \frac{12}{12} $$
$$ = 1 $$
| ノード番号 | 最大値との差 |
|---|---|
| 1 | 4 - 1 |
| 2 | 4 - 1 |
| 3 | 4 - 4 |
| 4 | 4 - 1 |
| 5 | 4 - 1 |
図2の場合
$$ GC_2 = \frac{(2 - 1) + (2 - 2) + (2 - 2) + (2 - 2) + (2 - 1)}{4^2 - 3 \times 4 + 2} $$
$$ = \frac{1}{6} $$
$$ = 0.166... $$
| ノード番号 | 最大値との差 |
|---|---|
| 1 | 2 - 1 |
| 2 | 2 - 2 |
| 3 | 2 - 2 |
| 4 | 2 - 2 |
| 5 | 2 - 1 |
演習問題5¶
spaCyを用いて、"She sings like an angel."と"You should try it too."を解析し、graphvizを用いて依存木を描いてみましょう。また、それぞれのグラフ中心性を求めてみましょう。
4.2 平均依存距離¶
- 単語の出現順序と依存関係を特徴量としたあたいです。
- 以下の文"You can send a leter to the library."では、
- "You"の出現順序は0、"You"が直接依存している"send"の出現順序は2です。
- つまり、この2つの単語の間にはひとつの単語が存在していいます。
- これを距離と考えて、"You"と"send"の依存距離は2とします。
- これをROOT以外ですべて計算し、ROOTを除く語数で割ったものを平均依存距離と言います。
- 一般的に平均依存距離の値が大きいほど文の理解が困難であると言われています。
import spacy
from spacy import displacy
nlp = spacy.load("en_core_web_sm")
import numpy as np
text = "You can send a letter to the library."
doc = nlp(text)
displacy.render(doc)
演習問題6¶
"You can send a letter to the library."の平均依存距離を算出してみましょう(ピリオドは除いて解析しましょう)。
- 木構造の深さを計算するとき、再帰関数が使われます。
- 再帰関数とは関数の中でその関数を呼び出す関数のことです。
- 以下に入力された値とその値より小さい自然数すべての総和を求める再帰関数を例として示します。
def total(n):
if n < 1:
return 0
return n + total(n - 1)
total(10)
55
- このtotal()という関数の計算プロセスを考えてみましょう。
- 入力は10なので、"if n <1:"のプロセスはスルーされ、10 + total(10 -1)が処理されます。
- 再度total()が呼び出され、入力が9なので"if n <1:"のプロセスはスルーされ、9 + total(9 -1)が処理されます。
- ここまでのプロセスをまとめると、10 + 9 + total(9-1)が処理されています。
- これが繰り返され、10 + 9 + 8 + 7 + total(7 - 1)のように続きます。
- nが1より小さくなるとif文が処理され、0が返されます。
- つまり、処理が繰り返され、10 + 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 + 0が処理され、その結果が返されます。
この、「ある条件が満たされるまで同じ処理が繰り返される」は、木の深さを測るというプロセスでも用いられます。
根から考えて、以下の処理を繰り返して進んだ距離を計測することで木の深さとすることができます。
- ノードに子があれば、(いずれかの)子ノードに進む
- ノードに子がなければ終了
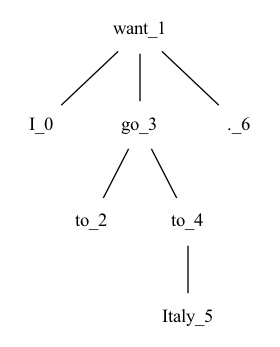
以下の木で、考えると"want_1"には子どもが3人います。
"want_1"から"I_0"までの深さは1で、"I_0"には子どもがいないので処理は終了します(深さ1)。
"want_1"から"go_3"までの深さは1で、"go_3"には子どもが2人います。"to_2"までの距離は1で、"to_2"には子どもがいないので処理は終了します(深さ2)。
このようにすべての単語に対して、処理を繰り返し、その最大値を得ることで木の深さを知ることができます。
def walk_tree(node, depth):
depths[node.orth_] = depth
if node.n_lefts + node.n_rights > 0:
return [walk_tree(child, depth + 1) for child in node.children]
text = "A boy climbed every tree."
doc = nlp(text)
depths = {}
for sent in doc.sents:
walk_tree(sent.root,0)
max(depths.values())
2
4.3.2 木の平坦さ¶
- 木の平坦さは、ROOTが直接統率する語の数です。
演習問題7¶
- "She was given a camera yesterday."と"I went to school by bus."の木の平坦さを算出してみましょう。