学習者言語の分析(応用)2(第5回)1
- 図2で示されるような、辺に向きがあるグラフもありますが、ここでは辺に向きがないグラフのみを扱います。
- 辺に向きがあるグラフを有向グラフといい、向きがないグラフを無向グラフと言います。
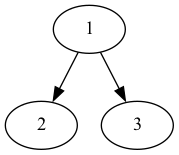 図2
図2
- 図3で示されているグラフのように、1組のノードが2本以上の辺で接続されている(多重辺)、あるいは、ひとつのノードをループする辺がある場合を一般グラフと言い、ここでは扱わないません。
- 多重辺およびループがないグラフを単純グラフと言います。
- ここで扱うグラフはすべて単純グラフです。
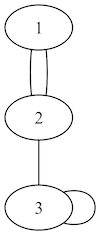 図3
図3
- 図4のグラフでは1~4で構成されているグラフから5、6で構成されているグラフに到達することができない。このようなグラフを非連結グラフと言い、ここでは扱わないません(2つのグラフとして扱います)。
- すべてのノードが連結されているグラフを連結グラフと言います。
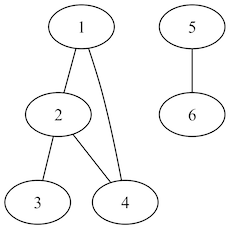 図4
図4
3.2 単純グラフの定義¶
- グラフ$G$を、点(node, vertex)の集合$V$と点を結ぶ辺(edge)の集合$E$のペアで、$G = (V,E)$と表します。
- 点のことを頂点、ノード、などと呼び、点を結ぶ線のことを辺、エッジ、アークなどと呼びます。
- 位数(order): 頂点の数
- 次数(degree): 頂点から出ている辺の数(図5の頂点1の次数は2)
- 部分グラフ: グラフの部分(例えば、図5の点1,2,3とそれらを結ぶ辺は全体の部分グラフ)
- 閉路(サイクル): ある点を選んで、辺を辿って、選んだ点に戻ってくることができる部分グラフ(図5の点1,2,4とそれらを結ぶ辺は全体の部分グラフは閉路)
- 橋(ブリッジ): 取り除くとグラフ全体が非連結になる辺(図5の点2と点3を結ぶ辺)
- 道(パス): 隣接する点を辿った経路
- 距離(最小距離): 2点間を移動するときに通る最小の辺の数(図5の点1から点3の距離は2)
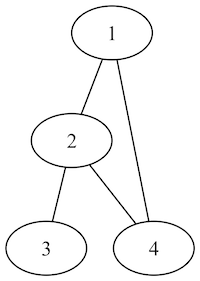 図5
図5
- 図5のグラフは以下のように集合で表現できます。
$$ V(G) = \{1,2,3,4\}$$
$$ E(G) = \{(1,2),(2,3),(2,4),(1,4)\}$$
- この授業では以下のように示すこととします。
In [1]:
V = [1,2,3,4]
E = [[1,2],[2,3],[2,4],[1,4]]
3.3 グラフの描画¶
- graphvizを用いてグラフを描画します。
In [2]:
# パッケージのimport
from graphviz import Graph
In [3]:
# インスタンスの生成
g = Graph()
# ノードに名前を付ける
g.node("1")
g.node("2")
g.node("3")
# エッジを描く
g.edge("1","2")
g.edge("1","3")
# グラフの出力
g
Out[3]:
- 以下のようにグラフが集合で表現された場合、forを用いてグラフを書きます。
In [4]:
V = ["1","2","3"]
E = [["1","2"],["1","3"]]
g = Graph()
for i in V:
g.node(i)
for j in E:
g.edge(j[0],j[1])
g
Out[4]:
3.4 同型¶
- 2つのグラフの$G_1$と$G_2$の点の間に一対一対応があり、$G_1$の任意の点を結ぶ辺の数が$G_2$対応する2点を結ぶ辺の数に等しいとき、$G_1$と$G_2$は同型といいます。
- $V(G_1) = V(G_2)$、$E(G_1) = E(G_2)$であれば$G_1$と$G_2$は同型です。
- 2つのグラフが同型であるかどうかを判定する方法は確定していないようです(?)。
- 本科目ではこの後で同型に近い考え方を利用します。
In [5]:
V = ["a","b","c","d"]
E = [["a","b"],["a","c"],["a","d"],["b","c"],["b","d"]]
g = Graph()
for i in V:
g.node(i)
for j in E:
g.edge(j[0],j[1])
g
Out[5]:
In [6]:
V = ["l","m","n","p"]
E = [["l","m"],["l","n"],["l","p"],["m","n"],["m","p"]]
g = Graph()
for i in V:
g.node(i)
for j in E:
g.edge(j[0],j[1])
g
Out[6]:
- 一般に、同型のグラフの次数列は同じですが、同じ次数列であってもグラフが同型とは限りません。
3.5 次数列¶
- すべてのノードの次数を降順で並べた数値の列を次数列と言います。
- グラフが同型であれば次数列は同じになりますが、次数列が同じグラフが必ず同型になるとは限りません。
- 図5の次数列は$(2,2,2,1)$になります。
 図5(再々掲)
図5(再々掲)
演習問題3¶
以下で定義されるグラフの次数列を求めてみましょう。
In [7]:
V = [1,2,3,4,5]
E = [[1,2],[2,3],[1,5],[2,4],[1,4],[3,5]]
3.6 木(根付き木)¶
- グラフの特別な形として以下のグラフを木(ツリー)と呼びます(図6)。
- 木には以下のような性質があります。
- 閉路がなく、$n - 1$の辺を持つ($n$はノードの数)。
- 連結で、$n - 1$の辺を持つ($n$はノードの数)。
- 連結で、すべての辺が橋である。
- 任意の2点を結ぶ道は1本しかない。
- 辺を1本足すと必ず閉路ができる。
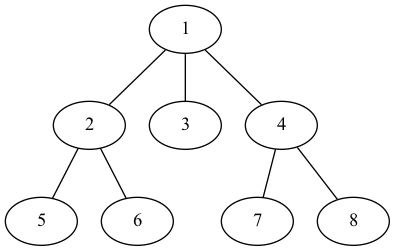 図6
図6
木において、ひとつの点を選び、それを 根(root) としグラフの中で一番「上」にあるとする。これを 根付き木 と呼びます。
図6において、点1を根とする根付き木とすると各名称が以下のようになります。
- 枝: 辺のこと
- 節点: 自分より下にノードがある頂点
- 葉: 自分より下にノードがない頂点
図5において頂点2と4は節点で、頂点3, 5, 6, 7,8は葉です。
家系図に見立てて以下のような関係に名前が付与されています。
- あるノードより根に近いノードを 先祖(ascendant) (図6のノード5にとってノード2,1は祖先)。
- あるノードより根から遠いノードを子孫 (descendant) (図6のノード1にとってすべてのノードは子孫)。
- あるノードに隣接し、そのノードより根に近いノードを親 (parent) (図6のノード7にとってノード4は親)。
- あるノードに隣接し、そのノードより根から遠いノードを子(child) (図6のノード4にとってノード7,8は子)。
- 親を共有するノードは兄弟(sibling) (図6のノード5,6は兄弟)。
根付き木では、根から葉までの距離を深さ(高さ) と呼ぶ。ある根付き木において最長の距離も深さと呼ぶ。
演習問題4¶
- spaCyを用いて"A boy climbed every tree."を解析し、その依存木を以下のように集合で表現してみましょう(単語に付与されている数字は出現順序です)。また、これらを用いてgraphvizで以下のような依存木を描いてみましょう。
V = ['A_0', 'boy_1', 'climbed_2', 'every_3', 'tree_4', '._5']
E = [['boy_1', 'A_0'], ['climbed_2', 'boy_1'], ['climbed_2', 'tree_4'], ['climbed_2', '._5'], ['tree_4', 'every_3']]
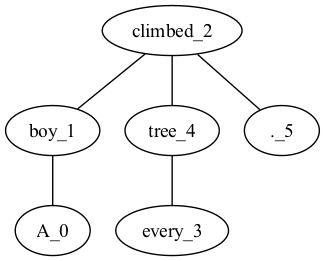 図7
図7
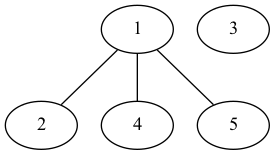 図1
図1