4.2 ニューラルネットワーク¶
- ニューラルネットワークは前回扱った機械学習(教師あり)の技法のひとつと考えることができます。
- 推論に基づく分散表現はニューラルネットワークの仕組みを利用したものです。
4.2.1 ニューラルネットワークの推論¶
- ニューラルネットワークは「学習」と「推論」の2つの段階に分けられます。
- ここでは「推論」に焦点を当てます(前回まで「予測」と呼んでいたプロセスです)。
- ニューラルネットワークとは「関数」の集合です。
- $ y = ax + b$という式にxを代入しyを得る場合、この式は関数です。
- ニューラルネットワークはこのような式がいくつか連なっているものと考えることができます。
- 例として、2つのデータを入力して、3つのデータを得るニューラルネットワークを考えてみましょう。
- 以下の図は◯がニューロン、ニューロンのつながりを→で表しています。
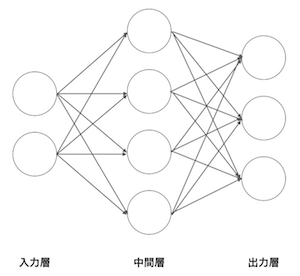
ニューロンはそれぞれ左から順番に入力層、中間層、出力層と呼びます。
矢印には重み(関数)があり、入力に重みをかけたものが次の層の入力になります。
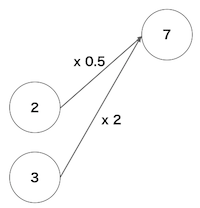
以下は上で示したニューラルネットワークの部分です。
この例では入力層の2と3にそれぞれの重み(0.5と2)かけたものが次の層の入力(7)になっています。
実際には前層の入力に影響を受けない定数を加算します。これをバイアスと呼びます(ここでは省略されています)。
- 実際のニューラルネットワークが行う計算の一部を数式で表して見ます。
- 入力層へ入力されるデータを$x_1,x_2$とし、重みを$w_{11},w_{21}$、バイアスを$b_1$とすると、中間層の一番上のニューロンへの入力を$h_1$とすると以下のようになります。
$$ h_1 = x_1w_{11}+x_2w_{21}+b_1 $$
- また、中間層の2番目のニューロンへの入力を$h_2$とし、その重みを$w_{12},w_{22}$、バイアスを$b_2$とすると、以下のようになります。
$$ h_2 = x_1w_{12}+x_2w_{22}+b_2 $$
- これらの計算を行列の積として以下のようにまとめて書くことができます。
$$ \begin{pmatrix} h_1 & h_2 \\ \end{pmatrix} = \begin{pmatrix} x_1 & x_2\\ \end{pmatrix} \begin{pmatrix} w_{11}\\ w_{21}\\ \end{pmatrix} + \begin{pmatrix} b_1 & b_2 \\ \end{pmatrix} $$
- 上の図の入力層から中間層への計算をまとめて以下のように書くことができます。
$$ \begin{pmatrix} h_1 & h_2 & h_3 & h_4 \\ \end{pmatrix} = \begin{pmatrix} x_1 & x_2\\ \end{pmatrix} \begin{pmatrix} w_{11} & w_{12} & w_{13} & w_{14}\\ w_{21} & w_{22} & w_{23} & w_{24}\\ \end{pmatrix} + \begin{pmatrix} b_1 & b_2 & b_3 &b_4 \\ \end{pmatrix} $$
- 中間層のへの入力$(h_1,h_2,h_3,h_4)$、入力$(x_1,x_2)$はベクトル、重み$(w_{1i},w_{2i})$は$2 \times 4$の行列なので、以下のように書くことができます。
$$ {\bf h} = {\bf xW} + {\bf b} $$
- それでは、10組の入力データをこのニューラルネットワークによって変換してみましょう。
import numpy as np
W1 = np.random.randn(2,4) # 重み
b1 = np.random.randn(4) # バイアス
x = np.random.randn(1,2) # 入力
h = np.dot(x,W1) + b1
h
array([[ 0.48247096, -1.2644639 , 2.33997006, 3.01376622]])
4.2.2 機械学習のモデルとしてのニューラルネットワーク¶
- ニューラルネットワークの推論における計算方法を学びました。
- では、実際に機械学習のモデルとしてニューラルネットワークがどう使われるのか見ていきましょう。
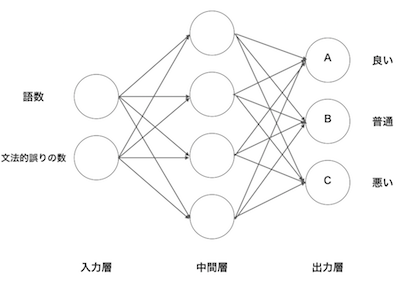
- 以下の図は、英語学習者の作文の評価を産出するニューラルネットワークのモデルです。
- 語数と文法的誤りの数を入力するとA,B,Cという出力が得られます。
- この出力を確率として扱えるように以下のように変換し、
$$ P(良い) = \frac{A}{A + B + C} $$
$$ P(普通) = \frac{B}{A + B + C} $$
$$ P(悪い) = \frac{C}{A + B + C} $$
- もっとも高い確率のカテゴリをその作文の評価とします。
- このようなモデルで評価を予測するためにはどうしたら良いでしょうか。
- あるいは、精度の高い予測モデルを作るにはニューラルネットをどのように評価すれば良いでしょうか。
4.2.3 損失関数¶
- 機械学習(教師あり)では、実際に人が付けた評価(良い、普通、悪い)があります。
- 損失関数とはニューラルネットの出力と人が付けた評価の差を以下の式で求めることができます。
- 以下の式は2乗和誤差と言います。
$$ E = \frac{1}{2}\sum_k(y_k - t_k)^2 $$
- ここで、$y_k$はニューラルネットの出力、$t_k$は人手が付けた評価を表し、kはデータの次元数(個数)を表ます。
- 例えば以下のような出力と評価があるとします。
y = [0.2,0.7,0.1]
t = [0,1,0]
- yはニューラルネットの出力、tは人手による評価で、それぞれ先頭の要素が「良い」、2番目の要素が「普通」、最後の要素が「悪い」の評価を表ています。
- ニューラルネットの出力はそれぞれの確率で、
- 人手による評価はone-hot表現で、この例では「普通」の評価が付与されています。
- 実際にこの例の2乗和誤差を計算すると以下のようになります。
\begin{equation*} \begin{split} E &= \frac{1}{2}\times(0.2 - 0)^2 + (0.7 - 1)^2 + (0.1 - 0)^2\\ & = 0.07\end{split} \end{equation*}
- 2乗和誤差を計算する関数を定義してみましょう。
import numpy as np
y1 = np.array([0.2,0.7,0.1])
t = np.array([0,1,0])
def mean_squared_error(y,t):
mse = 0.5 * np.sum((y-t)**2)
return mse
mean_squared_error(y1,t)
0.07000000000000002
- y2とtで損失を求めましょう。
y2 = np.array([0.5,0.3,0.2])
- 2乗誤差と同様よく用いられる損失関数として交差エントロピー誤差があります。
- 交差エントロピー誤差は以下の式で定義されます。
$$ E = - \sum_k t_k log y_k$$
- 交差エントロピー誤差を計算する関数を定義してみましょう。
- log(0)は計算できないため、deltaという変数に非常に小さい値を入れて対処します。
def cross_entropy_error(y,t):
delta = 1e-7
cee = -np.sum(t * np.log(y + delta))
return cee
- y1とt、y2とtの交差エントロピー誤差を求めてみましょう。
データがたくさんある場合
損失関数を用いてニューラルネットワーク(NN)の重みを更新し、精度の高い予測をします。
教師ラベル(人手による評価)が付与されたデータに対する損失関数を求め、
その値をできるだけ小さくする重みを探します。
先ほど学んだ損失関数はひとつ(1組)のデータにおける損失関数でした。
データが100個ある場合、100個の損失関数の和を求めます。
$$ E = - \frac{1}{N} \sum_n\sum_k t_{nk} log y_{nk}$$
- データが$N$個あって、$t_{nk}$は$n$個目のデータの$k$次元目の値を意味します。
- この式を定義すると以下のようになります。
import numpy as np
def cross_entropy_error(y,t):
cee = - np.sum(t * np.log(y))/y.shape[0]
- 以下のデータの交差エントロピー誤差を計算してみましょう。
y = np.array([[0.1,0.2,0.7],[0.5,0.2,0.3]])
t = np.array([[1,0,0],[1,0,0]])
4.2.4 ニューラルネットワークにおける勾配¶
- 勾配(降下)法を用いてニューラルネットワークの重みとバイアスを更新し、精度の高い予測が可能なニューラルネットワークを構築します。
- ここで求める勾配とは重みに対する損失関数の勾配です。
- $2 \times 3$の重み$\bf{W}$だけを持つニューラルネットワークを例として考えます。
- この損失関数を$L$で表すと勾配は$\frac{\partial L}{\partial\bf W}$となり、数式で表すと以下のうようになります。
$$ \bf{W} = \begin{pmatrix} w_{11} & w_{12} & w_{13}\\ w_{21} & w_{22} & w_{23}\\ \end{pmatrix} $$
$$ \frac{\partial L}{\partial\bf W} = \begin{pmatrix} \frac{\partial L}{\partial w_{11}} & \frac{\partial L}{\partial w_{12}} & \frac{\partial L}{\partial w_{13}}\\ \frac{\partial L}{\partial w_{21}} & \frac{\partial L}{\partial w_{22}} & \frac{\partial L}{\partial w_{23}}\\ \end{pmatrix} $$
- $\frac{\partial L}{\partial\bf W}$の各要素はそれぞれの要素の偏微分です。
- $\frac{\partial L}{\partial w_{11}}$は$w_{11}$が変化すると損失関数$L$がどれだけ変化するかということを表しています。
- 以下のクラスは出力を求めるメソッドと損失関数を求めるメソッドを持つニューラルネットワークです。
# 交差エントロピー誤差
def cross_entropy_error(y,t):
cee = - np.sum(t * np.log(y))/y.shape[0]
return cee
# softmax関数
def softmax(a):
c = np.max(a)
exp_a = np.exp(a - c)
sum_a = np.sum(exp_a)
y = exp_a / sum_a
return y
import numpy as np
class simpleNet:
def __init__(self):
self.W = np.random.randn(2,3)
def predict(self,x):
return np.dot(x,self.W)
def loss(self,x,t):
z = self.predict(x)
y = softmax(z)
loss = cross_entorypy_error(y,t)
return loss
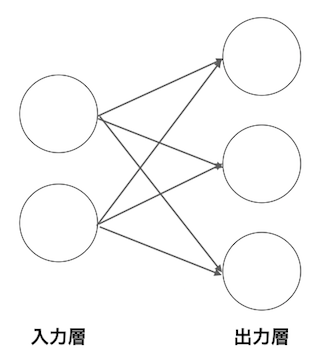
- このニューラルネットは以下のような構造になっています。
- 入力が2つで出力が3つです。
- バイアスは省略します。
- __init__()で重みを初期化します(ランダムな値を生成します)。
- 入力が2つで出力が3つなので重みは$2 \times 3$の行列になります。
- predict()は入力(x)に重みをかけます。
- loss()は入力と重みの掛け算の結果をsoftmax()を利用して確率に変換し、
- cross_entropy_error()を利用して損失を求めます。
- それではsimpleNetを使ってみましょう。
# インスタンスの生成
sn = simpleNet()
# インスタンスを生成させると、重みにランダムな値が入ります(初期化)。以下のように確認できます。
sn.W
array([[ 1.72265811, 0.68672941, 1.10772301],
[ 0.60344169, 0.60322389, -0.3536039 ]])
# 掛け算(推論)
x = np.array([2.0,3.0])
sn.predict(x)
array([5.25564131, 3.1831305 , 1.15463432])
# 正解ラベル
t = np.array([0,0,1])
# 損失の計算
sn.loss(x,t)
1.4113868299245542
- 以下のnumerical_gradient()を利用して勾配を求めます(拡張しました)。
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
while not it.finished:
idx = it.multi_index
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 値を元に戻す
it.iternext()
return grad
- numerical_gradient()は引数として関数を実行するため以下のように新たな関数を定義します。
def f(W):
return sn.loss(x,t)
- numerical_gradient()で勾配を計算してみましょう。
numerical_gradient(f,sn.W)
array([[ 0.58355381, 0.07345154, -0.65700535],
[ 0.87533072, 0.11017731, -0.98550803]])
- この結果は、例えば、$\bf W$の$w_{11}$は$0.583...$なので$w_{11}$を$h$増やすと損失関数は$0.58h$増加することを意味します。
- 一方で$w_{23}$の値は$-0.98...$なので、$w_{23}$を$h$増やすと損失は$-0.98h$減ります。
- なので、損失を減らすためには$w_{23}$の値(重み)を増やし$w_{11}$を減らす方向へ更新します。