学習者言語の分析（応用）1（第4回）

  • 4.1 ニューラルネットワークを理解するための前提
    • 4.1.1 クラス
    • 4.1.2 和記号の復習
    • 4.1.3 ベクトルと行列
    • 4.1.4 ベクトルの内積と行列の積
    • 4.1.5 シグモイド関数
    • 4.1.6 数値微分
    • 4.1.7 偏微分
    • 4.1.8 勾配
    • 4.1.9 勾配（降下）法
    • 4.1.10 softmax関数

4.1 ニューラルネットワークを理解するための前提¶

4.1.1 クラス¶

  • ここまで扱ってきた数値、文字列、リストには「クラス」という設計図から作られたオブジェクト（変数）です。
  • オブジェクトとはデータとメソッドを持つものと言えます。
  • 以下の文字列型のオブジェクトには"YOUNGER GENERATION"というデータとlower()やlen()などのメソッドを持っています。
In [3]:
# 以下の文字列型のオブジェクトには"YOUNGER GENERATION"
# というデータとlower()やlen()などのメソッドを持っています。

a = "YOUNGER GENERATION"

a.lower()
Out[3]:
'younger generation'
  • このようなクラスという「設計図」を自分で作ることができます。
  • 以下は能力と運と貯金額を受け取って貯蓄シミュレーションをするクラスです。
In [15]:
import numpy as np
In [54]:
class Human:
    def __init__(self,x,y,z):
        self.ability = x
        self.fortune = y
        self.saving = z

    def work(self):
        self.saving += 100 * self.ability

    def incident(self):
        if np.random.binomial(1,self.fortune) > 0:
            self.saving += 200
        else:
            self.saving -= 100
In [57]:
L = [0,0,0,0,0,0,0,1,1,1]
John = Human(1.2,0.3,100)
In [58]:
for i in range(35):
    d = np.random.choice(L,1)
    if d == 0:
        John.work()
    else:
        John.incident()

John.saving
Out[58]:
2060.0
  • 最初のメソッド(def __init__)はこのクラスを初期化します。能力(x)、運(y)、デフォルトの貯金額(z)を保存します。
  • work()は1年間働いて貯金できる金額です。
  • incident()は何かしら偶発的なイベントです。運が良ければ例年の倍の額を貯金できますが、運が悪いと貯金額が-100になります。

4.1.2 和記号の復習¶

  • $\sum$（シグマ、和記号)は単なる和
  • $ \sum_{i=0}^n x_i^2$を
  • データ: [12,25,32,65,44,89,35]
  • でやってみると
  • $ \sum_{i=0}^n x_i^2 = 12^2 + 25^2 + 32^2 + ... 35^2$

4.1.3 ベクトルと行列¶

  • ニューラルネットワークにおける計算はすべてベクトル、行列の計算です。
  • ベクトルとは大きさと向きを持った量です。
  • Pythonでは１次元のリストとして扱います。
  • 行列は２次元に並んだ数の集まりです。
  • 行列の横方向の並びを行、縦方向の並びを列と呼びます。
  • 以下の図の行列は３行２列の行列と呼び、　$3 \times 2$の行列と表記します。 vector_matrix
  • それではNumPyを利用してベクトルと行列を扱ってみましょう。
In [6]:
import numpy as np
In [7]:
# ベクトル
x = np.array([1,2,3])
x
Out[7]:
array([1, 2, 3])
In [8]:
# 行列
W = np.array([[1,2,3],[4,5,6]])
W
Out[8]:
array([[1, 2, 3],
       [4, 5, 6]])
In [9]:
# 行数と列数
W.shape
Out[9]:
(2, 3)

4.1.4 ベクトルの内積と行列の積¶

  • 2つのベクトル$\vec{x}, \vec{y}$の内積は内積は以下のように定義されます。

$$ \vec{x} \cdot \vec{y} = x_1 y_1 + x_2 y_2 \cdots + x_n y_n$$

  • 上記の式は、2つのベクトル$ \vec{x} = (x_1, \cdots,x_n)$と$ \vec{y} = (y_1, \cdots,y_n)$の対応する要素の積を足し合わせてものです。

  • 内積はベクトル同士がどれぐらい同じ方向を向いているかという指標になります。

  • 行列の積は左側の行列の行ベクトルと右側の行列の列ベクトルの内積によって計算されます。

  • 以下の例の場合、左側の行列の1行目と右側の行列の１列目の内積が、計算結果の行列の1行1列目に格納されます。


$$ \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix} \begin{pmatrix} 5 & 6 \\ 7 & 8 \\ \end{pmatrix} = \begin{pmatrix} 19 & 22 \\ 43 & 50 \\ \end{pmatrix} $$


  • 結果の行列の1行１列の19は$ 1 \times 5 + 2 \times 7$の計算結果です。
  • 同様に2行２列の50は$6 \times 3 + 4 \times 8 $の計算結果です。
  • pythonではベクトルの積、行列の積を以下のように扱います。
In [10]:
# ベクトルの内積
a = np.array([1,2,3])
b = np.array([4,5,6])

np.dot(a,b)
Out[10]:
32
In [11]:
# 行列の積
a = np.array([[1,2],[3,4]])
b = np.array([[5,6],[7,8]])

np.dot(a,b)
Out[11]:
array([[19, 22],
       [43, 50]])
  • 行列の積は、掛け合わせる左側の行列の列数と右側の行列の行数が一致してなければなりません。
  • $3 \times 2$行列と$2 \times 4$行列の積は計算できますが、$3 \times 2$行列と$4 \times 4$行列の積は計算できません。

4.1.5 シグモイド関数¶

  • ニューラルネットワークでよく使用される関数です。
  • 以下のように定義されます。

$$ f(x) = \frac{1}{1+exp(-x)} $$

  • $ exp(-x)$は$e^{-x}$を意味します。
  • Pythonの関数で定義すると以下のようになります。
In [15]:
import numpy as np

def sigmoid(x):
    return 1/(1+np.exp(-x))
  • シグモイド関数は以下のような形の関数です。
In [16]:
import matplotlib.pyplot as plt
%matplotlib inline

x = np.arange(-3,3,0.05)
y = sigmoid(x)
plt.plot(x,y)
Out[16]:
[<matplotlib.lines.Line2D at 0x116920580>]
No description has been provided for this image
  • 以下のように使います。
In [17]:
x_1 = np.array([-1.0,1.0])
sigmoid(x_1)
Out[17]:
array([0.26894142, 0.73105858])
In [18]:
x_2 = np.array([[1,2,3],[-1,-2,-3]])
sigmoid(x_2)
Out[18]:
array([[0.73105858, 0.88079708, 0.95257413],
       [0.26894142, 0.11920292, 0.04742587]])

4.1.6 数値微分¶

  • 微分とはある瞬間の変化の量を表たもので以下の式で定義されます。

$$ \frac{df(x)}{dx} = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$

  • ある関数$y = f(x)$において、$x$に関する$y$の微分は$\frac{dy}{dx}$と書きます。これは$x$の値を少しだけ変化させたとき、$y$がどれだけ変化するかという「変化の割合」です。
  • それではPythonで微分を求める関数を定義しましょう。
In [19]:
def numerical_diff(f,x):
    h = 1e-4 # 0.0001
    nd = (f(x+h) - f(x-h))/(2 * h)
    return nd
    
# 微分の定義式と異なりますが、実際に計算すると誤差が大きく
# なるためこのように定義します。
# ちなみに、定義式は前方差分と言い、この式は中心差分と言います。
  • それでは以下の2次関数を実際に微分してみましょう。

$$ y = 0.01x^2 + 0.1x$$

  • この式をPythonで書くと以下のようになります。
In [20]:
def func_1(x):
    return 0.01*x**2 + 0.1*x
  • この関数を描画してみましょう。
In [21]:
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
x = np.arange(0.0,20.0,0.1) # 0から20まで0.1刻みのベクトルを生成

y = func_1(x)

plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x,y)
Out[21]:
[<matplotlib.lines.Line2D at 0x116a1a5b0>]
No description has been provided for this image
  • この関数の微分を$x = 2$のとき、$x = 10$のときで計算してみましょう。
In [22]:
numerical_diff(func_1,2)
Out[22]:
0.14000000000014
In [23]:
numerical_diff(func_1,10)
Out[23]:
0.2999999999986347
  • $ y = 0.01x^2 + 0.1x$の微分$\frac{dy}{dx}$の解析的な解は、$0.02x+0.1$なので
  • $x = 2$の「真の微分」は$0.14$
  • $x = 10$の「真の微分」は$0.3$
  • なので、一致はしませんがその差はかなり小さいと言えます。

4.1.7 偏微分¶

  • 次に以下のような変数が２つある関数の微分について考えます。

$$ f(x_0,x_1) = x_0^2 + x_1^2$$

  • この式をPythonでは次のうように定義することができます。
In [24]:
def func_2(x):
    return x[0]**2 + x[1]**2

# 2つの引数をリストで受け取ります。

func_2([1,2])
Out[24]:
5
  • この関数を可視化すると以下のようになります。
In [25]:
import matplotlib.pyplot as plt
%matplotlib inline

x0 = np.arange(-3.0,3.0,0.1)
x1 = np.arange(-3.0,3.0,0.1)
X = [x0,x1]
xx0,xx1 = np.meshgrid(x0,x1)
y = func_2([xx0,xx1])

fig = plt.figure()
ax = fig.add_subplot(projection="3d")

ax.set_xlabel("$x_0$")
ax.set_ylabel("$x_1$")
ax.set_zlabel("$f(x_0,x_1)$")
ax.plot_surface(xx0,xx1,y,)
Out[25]:
<mpl_toolkits.mplot3d.art3d.Poly3DCollection at 0x116ab0cd0>
No description has been provided for this image
  • この$ f(x_0,x_1) = x_0^2 + x_1^2$という関数には$x_0$と$x_1$という変数が2つあるため、どちらの変数に対しての微分なのかを区別する必要があります。
  • ここで扱うような関数（複数の変数からなる関数）の微分を偏微分と言います。
  • この偏微分は、$\frac{\partial f}{\partial x_0}$、$\frac{\partial f}{\partial x_1}$と書きます。
  • $ x_0 = 3$、$x_1 = 4 $のときの$x_0$に対する偏微分$\frac{\partial f}{\partial x_0}$を求めましょう。
In [26]:
# x_1を4に固定した新たな関数を定義する
def func_x0(x):
    return x**2 + 4**2

# x0が3のときの微分を求める
numerical_diff(func_x0,3)
Out[26]:
6.00000000000378
  • $ x_0 = 3$、$x_1 = 4 $のときの$x_1$に対する偏微分$\frac{\partial f}{\partial x_1}$を求めましょう。
  • このように、偏微分は1変数の微分と同じで、ある場所の傾きを求めます。ただし、偏微分の場合、複数ある変数の中で対象とする変数を一つにし、他の変数はある値に固定します。

4.1.8 勾配¶

  • 先の例では$x_0$と$x_1$の偏微分をそれぞれの変数ごとに計算しました。
  • ですが、これらの偏微分をまとめて計算したい時もあります。
  • 例えば、$x_0 = 3$、$x_1 = 4$の時の$(x_0,x_1)$の両者の偏微分をまとめて、$(\frac{\partial f}{\partial x_0},\frac{\partial f}{\partial x_1})$ のように。
  • このように偏微分をベクトルとしてまとめたものを勾配と言います。
  • 以下は勾配を計算するために定義した関数です。
In [27]:
import numpy as np

def numerical_gradient(f,x):
    h = 1e-4
    grad = np.zeros_like(x)
    
    for idx in range(x.size):
        tmp_val = x[idx]
        
        # f(x+h)の計算
        x[idx] = tmp_val + h
        fxh1 = f(x)
        
        #f(x-h)の計算
        x[idx] = tmp_val - h
        fxh2 = f(x)
        
        grad[idx] = (fxh1 - fxh2) / (2*h)
        x[idx] = tmp_val # 値を元に戻す
    
    return grad

  • この関数の引数(f,x)において、fは$ y = x_2$のような式、xはfで与えられた式において偏微分を求めたい点のリスト（配列）です。

  • x.sizeはxの大きさを返します。

  • np.zeros_like()は引数と同じサイズですべての要素が0の配列を生成します。

  • tmp_val = x[idx]で偏微分を求めたい点をtmp_valに保存します。

  • x[idx] = tmp_val + hで偏微分を求めたい点x[idx]にその点をhだけ動かした値を代入します。

  • fxh1 = f(x)とfxh2 = f(x)はそれぞれh分だけ動かした値

  • grad[idx] = (fxh1 - fxh2) / (2*h)で各点の微分を求めて保存する。

  • numerical_gradient()を使って、以下の関数の点、(3,4)、(0,2)、(3,0)での勾配を求めてみましょう。

In [28]:
def func_2(x):
    return x[0]**2 + x[1]**2
In [29]:
numerical_gradient(func_2,np.array([1.5,1.0]))
Out[29]:
array([3., 2.])
  • この勾配（というベクトル）は対象とする関数の値が最小となる方向を示しています。
  • 以下のグラフは$ f(x_0,x_1) = x_0^2 + x_1^2$の勾配（にマイナスをかけたもの）を示したものです。

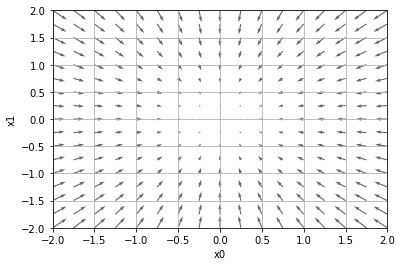
gradient_2d

  • このベクトル（勾配）は各点に置いて関数の値を最も減らす方向を示しています。

4.1.9 勾配（降下）法¶

  • 勾配法とは、

    • 対象とする関数の値が小さくなるようにその変数を勾配が示す方向に一定距離だけ進め、
    • さらに移動した点でも同様に勾配を求め、また、その勾配が示す方向へ進むというように繰り返して、
    • 最適な変数を探す方法です。

  • 勾配法は以下のように表すことができます。

$$ x_0 = x_0 - \eta \frac{\partial f}{\partial x_0}$$ $$ x_1 = x_1 - \eta \frac{\partial f}{\partial x_1}$$

  • 式中の$\eta$は更新する量（距離）に対する重みづけで、学習率(learning rate)と言います。
  • この値が大きいと1回の更新（学習）で進む距離が長くなります。
  • 勾配（降下）法を定義すると以下のようになります。
In [30]:
def gradient_descent(f,init_x,lr=0.01,step_num=50):
    x = init_x
    for i in range(step_num):
        grad = numerical_gradient(f,x)
        x -= lr * grad
    return x
  • 引数のfはパラメターの最小値を求めたい関数
  • init_xは初期値
  • lrは学習率(learning rate)
  • step_numはこの処理の繰り返し回数
In [31]:
init_x = np.array([1.0,2.0])
gradient_descent(func_2,init_x=init_x,lr=0.1,step_num=100)
Out[31]:
array([2.03703598e-10, 4.07407195e-10])

4.1.10 softmax関数¶

  • A, B, Cが起きる頻度の総和でAの頻度を割るとAが起きる確率と捉えることができます。

$$ P(A) = \frac{A}{A + B + C} $$

  • これを頻度ではないもの（A, B, Cに負の値が入る場合など）にも拡張して確立を求めるためにsoftmax関数と呼ばれる関数を使用します($e^x$は常に非負なので）。

$$ y_k = \frac{exp(a_k)}{\sum_k exp(a_i)}$$

  • $exp(x)$は$e^x$を表す指数関数で、$e$は2.7182（ネイピア数）です。
  • この式をそのまま実装するとオーバーフローと言ってコンピュータが計算できない大きな値($e^{1000}$はinf)になることがあるので以下のようにすべて値から最大値を引いて計算します。

$$ y_k = \frac{exp(a_k - a_{max})}{\sum_k exp(a_i - a_{max})}$$

  • これを確率のように扱います。

  • 以下のように定義します。

In [14]:
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_a = np.sum(exp_a)
    y = exp_a / sum_a
    
    return y
  • $e^x$のグラフを以下に示します。
In [12]:
# e^xのグラフ
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

x = np.arange(0,5.0,0.1)
y = np.exp(x)
plt.plot(x,y)
Out[12]:
[<matplotlib.lines.Line2D at 0x10983f280>]
No description has been provided for this image
  • softmax()は以下のように使います。
In [15]:
a = np.array([0.3,2.9,4.0])
softmax(a)
Out[15]:
array([0.01821127, 0.24519181, 0.73659691])