学習者言語の分析（応用）1（第3回）

  • 3.3 機械学習（教師あり）のさまざまな手法
    • 3.3.1 決定木
    • 3.3.2 サポートベクターマシン(Support Vector Machine: SVM)

3.3 機械学習（教師あり）のさまざまな手法¶

  • 機械学習（教師あり）にはさまざまな手法が提案されていますが、基本的には3.1で述べた考え方に基づいています。
  • ここでは代表的なものを２つ紹介します。

3.3.1 決定木¶

  • 決定木とは以下のような木構造を用いてデータを分類します。
  • 以下の図の□で示されている所にYes/Noで答えられる質問に答える形でデータを分類します。

fig1

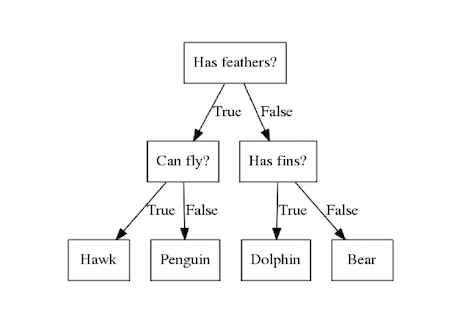
  • 決定木では、データの特徴からこのチャートを生成します。
  • 決定木では、データを綺麗に分割する点を見つけることを繰り返し、このチャートを生成します。
  • その際に不純度（diversity）という概念を用います。
  • 不純度とはどれだけ混ざっているかを示す指標です。
  • ここではジニ不純度（Gini's Diversity Index）を用いて不純度を算出します。
  • ジニ不純度$I_G(t)$は以下の式で求められます。

$$I_G(t) = 1 - \sum_{i=1}^c p(i|t)^2$$

  • $I_G(t)$の$t$は決定木の任意のノードを、cはカテゴリ数を示し、$p(i|t)$は、当該ノード のデータの総数に対するあるカテゴリに属するデータの割合を示します。
  • 100人の受験者がいて、合格した人と不合格した人が50人ずついるとして，上記の式に当てはめると，ジニ不純度は以下の式で計算すると0.50となります。 $$ I_G(t) = 1 - \{(\frac{50}{100})^2 + (\frac{50}{100})^2\}$$
  • この100人の模擬試験のX点で分けるとX点以下のグループには合格者が4人、不合格者が42人で、X点以上のグループには合格者が46人、不合格者が8人いました。
  • このとき、以下に示すようにX点以上のグループのジニ不純度は0.16となります。

$$ I_G(t) = 1 - \{(\frac{4}{100})^2 + (\frac{42}{100})^2\}$$ $$ = 0.16 $$

  • また、X点以下のグループのジニ不純度は0.25になります。 $$ I_G(t) = 1 - \{(\frac{46}{100})^2 + (\frac{8}{100})^2\}$$ $$ = 0.25 $$
  • この時点で、分割後のそれぞれのグループのジニ不純度は分割前のジニ不純度より小さくなっています。
  • この分割でどの程度不純度が減少したかを分割前と分割後で比較するために、分割後のそれぞれのジニ不純度にそれぞれの分割の割合をかけて分割前の不純度から引きます。これを情報利得と呼びます。
  • 分割前を$D_p$，分割後のそれぞれのグループを$D_L$，$D_R$とし，分割前のデータの数を$N_p$、分割後の2つのグループのデータの数を$N_L$、$N_R$とし，分割に用いたデータ（模擬試験の点数）を$f$とした場合，この分割の情報利得$I_G(D_p,f)$は以下の式で求められます。

$$I_G(D_p,f) = I_G(D_p) - \frac{N_L}{N_P}I_G(D_L) - \frac{N_R}{N_P}I_G(D_R)$$

  • 情報利得は分割後のジニ不純度が小さくなれば小さくなるほど大きくなります（この例での情報利得は0.04になります）。
  • このように情報利得が最大になるような特徴量の分割点の探索を繰り返し，予測方法を決定します。
  • ここまでの説明を可視化すると以下のようになります。
In [1]:
import mglearn
In [2]:
mglearn.plots.plot_tree_progressive()
No description has been provided for this image
No description has been provided for this image
No description has been provided for this image
No description has been provided for this image
  • 学習者の作文から抽出した特徴量を用いて作文の評価を予測します。
In [3]:
# データの読み込み
import pandas as pd
data = pd.read_csv("../DATA01/TALL030302.csv",index_col=0)
data.head()
Out[3]:
sents words wps ttr score
JPN002 25 392 15.680000 0.725000 3
JPN004 18 288 16.000000 0.558333 3
JPN006 26 548 21.076923 0.716667 5
JPN008 21 332 15.809524 0.583333 3
JPN010 18 391 21.722222 0.583333 3
  • 英語学習者が書いた作文から、文の数、単語の数、一文あたりの平均語数(wps)、異なり語の割合(ttr)を用いて評価(score)を予測します。
In [4]:
# モジュールのインポートとモデルの作成
from sklearn.tree import DecisionTreeClassifier

# train_test_splitのインポート
from sklearn.model_selection import train_test_split

# データの分割
X_train,X_test,y_train,y_test = train_test_split(data[["sents","words","wps","ttr"]],data["score"],test_size=0.2,random_state=0)

# インスタンスの生成
clf = DecisionTreeClassifier(max_depth=2)

# 学習
clf = clf.fit(X_train,y_train)

# 予測精度の出力
clf.score(X_test,y_test)
Out[4]:
0.48

3.3.2 サポートベクターマシン(Support Vector Machine: SVM)¶

  • 線（あるいは面）によって2クラスを分類する方法
  • 以下の図では▲と●で2つのクラスを表しています。
  • 図Aのように特徴量1のみを用いて2つのクラスを分類しています。
  • 図Bでは特徴量1と２の両方を用いて2つのクラスを分類しています。

fig1

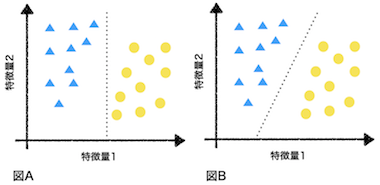
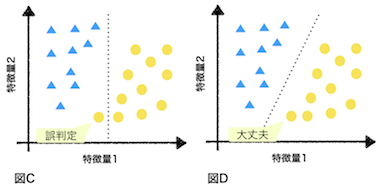
  • サポートベクターマシンは、それぞれのクラスのデータからの距離が最大になる直線を求めます。
  • この目的に基づくと図Aの直線より図Bの直線の方が良いと言えます。

fig1

In [5]:
# 決定木による予測で用いたデータと同じデータを使用する。

# モジュールのインポート
from sklearn import svm

# インスタンスの生成
clf = svm.SVC()

# 学習
clf.fit(X_train,y_train)

# 精度の出力
clf.score(X_test,y_test)
Out[5]:
0.44