学習者言語の分析（応用）第3回

• 3.1 機械学習（教師あり）の基本的な考え方
• 3.2 交差検証法

3.1 機械学習（教師あり）の基本的な考え方

• ある資格試験があり、その模擬試験の結果から資格試験の合否を予測することを考えます。
• 以下のようなデータが得られたとします。

# 模擬試験の点数
D = [110,120,150,190,210,215,240,255,270,280,290,300,305,310,350,370,375,400,405]
# 合否(0が不合格、1が合格)
S = [0,0,0,0,0,0,1,0,1,0,1,0,1,1,1,1,1,1,1]

import pandas as pd

df = pd.DataFrame({"点数":D,"合否":S})
df

	点数	合否
0	110	0
1	120	0
2	150	0
3	190	0
4	210	0
5	215	0
6	240	1
7	255	0
8	270	1
9	280	0
10	290	1
11	300	0
12	305	1
13	310	1
14	350	1
15	370	1
16	375	1
17	400	1
18	405	1

• 以下の図は、数直線上に模擬試験の点数を表したものです。
• 青が合格、ピンクが不合格を示しています。

• このデータにおいて点数に基づいてどこで受験者を分ければ、最も間違いが少ない予想となるかを考えます。
• 以下の図の赤い矢印で示したあたりで受験者を分けて、矢印の左側にいる受験者を不合格、右側にいる受験者を合格と予想すると最も間違いが少なくなります。
• この、既存のデータを分析して、予測方法を得る段階を学習と呼びます。

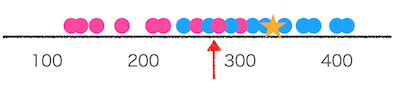
• また、上の図の★は新たに得られたデータで合否が未知だとします。
• このデータは赤い矢印の右側にあるので合格と予測します。
• この段階を予測と呼びます。

• このプロセスを実際にやってみましょう。

# 模擬試験の点数
D = [110,120,150,190,210,215,240,255,270,280,290,300,305,310,350,370,375,400,405]
# 合否(0が不合格、1が合格)
S = [0,0,0,0,0,0,1,0,1,0,1,0,1,1,1,1,1,1,1]

# データのそれぞれの値に関して、赤い矢印を100から410まで5点刻みで動かした場合の予測を算出する
A = []

for i in range(100,415,5):
    tmp = []
    for j in D:
        if j < i:
            tmp.append(0)
        else:
            tmp.append(1)
    A.append(tmp)

# 赤い矢印を100から410まで動かしたそれぞれの場合の正解率を算出
R = []

for i in A:
    tmp = []
    for j,k in zip(i,S):
        if j == k:
            tmp.append(1)
        else:
            tmp.append(0)
    r = sum(tmp)/len(tmp)
    R.append(r)

# 可視化
import matplotlib.pyplot as plt
%matplotlib inline

L = list(range(100,415,5))
plt.plot(L,R)
plt.xlabel("the position of the arrow")
plt.ylabel("accuracy rate")

Text(0, 0.5, 'accuracy rate')

• このデータでは200点から300点までの間の複数の点で最も高い正解率が得られます。

3.2 交差検証法

• 上の方法で決めた赤い矢印の位置でデータを分類すると85%の精度でデータを正しく分類することができます。
• しかし、この精度は答え（合否に関する情報）を知っていて予測した場合の精度です。
• これをこの予測方法の精度として採用することはできません。
• 知りたいのは、「未知」のデータにおける予測精度です。
• 交差検証法とはデータを学習データとテストデータに分割し、学習データで「学習」し、テストデータで予測精度を計算する方法です。

# 交差検証法のパッケージをimport
from sklearn.model_selection import train_test_split

# データを学習データとテストデータに分割
X_train, X_test, Y_train, Y_test = train_test_split(D, S, test_size=0.5,random_state=0)

# 学習データで学習1
A2 = []

for i in range(100,415,5):
    tmp = []
    for j in X_train:
        if j < i:
            tmp.append(0)
        else:
            tmp.append(1)
    A2.append(tmp)

# 学習データで学習2
R2 = []

for i in A2:
    tmp = []
    for j,k in zip(i,Y_train):
        if j == k:
            tmp.append(1)
        else:
            tmp.append(0)
    r = sum(tmp)/len(tmp)
    R2.append(r)

# 最大値を取るindex
R2.index(max(R2))

41

# 最大値を取る赤い矢印の位置
L[41]

305

# テストデータで予測精度の確認
R3 = []

for i in X_test:
    if i < 305:
        R3.append(0)
    else:
        R3.append(1)

# 正解率
n = 0
for i,j in zip(R3,Y_test):
    if i == j:
        n +=1
print(n/len(R3))

0.7