2.1 頻度に基づいた分散表現¶
- 前回の授業では、ヒエログリフに出現する名詞と動詞の共起頻度に基づいて名詞を以下のように数値列で表現しました。
label = ["knife","cat","???","boat","cup","pig","banana"]
C = [[51,20,84,0,3,0],
[52,58,4,4,6,26],
[115,83,10,42,33,17],
[59,39,23,4,0,0],
[98,14,6,2,1,0],
[12,17,3,2,9,27],
[11,2,2,0,18,0]]
# Standardization
C2 = []
for c in C:
sum_c = sum(c)
D = []
for c2 in c:
D.append(c2/sum_c)
C2.append(D)
import pandas as pd
pd.options.display.precision = 3
table = pd.DataFrame({"knife":C2[0],"cat":C2[1],"???":C2[2],"boat":C2[3],"cup":C2[4],"pig":C2[5],"banana":C2[6]},index=["get","see","use","hear","eat","kill"])
Decipher_hieroglyphs = table.T
Decipher_hieroglyphs
| get | see | use | hear | eat | kill | |
|---|---|---|---|---|---|---|
| knife | 0.323 | 0.127 | 0.532 | 0.000 | 0.019 | 0.000 |
| cat | 0.347 | 0.387 | 0.027 | 0.027 | 0.040 | 0.173 |
| ??? | 0.383 | 0.277 | 0.033 | 0.140 | 0.110 | 0.057 |
| boat | 0.472 | 0.312 | 0.184 | 0.032 | 0.000 | 0.000 |
| cup | 0.810 | 0.116 | 0.050 | 0.017 | 0.008 | 0.000 |
| pig | 0.171 | 0.243 | 0.043 | 0.029 | 0.129 | 0.386 |
| banana | 0.333 | 0.061 | 0.061 | 0.000 | 0.545 | 0.000 |
- これが単語の分散表現です。
- しかしながら、この方法だと文における単語の役割が分かっていないとできません。
2.2 コンテクストを用いた分散表現¶
- この授業で「文脈(コンテクスト)」と言った場合には、対象の単語の周囲にある単語のことを指します。
- また、コンテクストのサイズをウィンドウサイズと言い、
- ウィンドウサイズが1の場合は対象単語の左右1単語を指します。
- 以下の文で、"Force"のウィンドウサイズ1のコンテクストは"the"と"will"です。
- Remember, the Force will be with you, always.
- この文に出現する単語をこの手法を用いてベクトル化(数値の列にすること)すると以下のようになります。
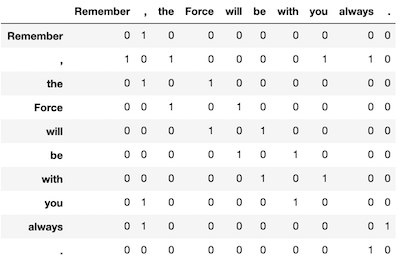
- この手法は対象となる文(文章)に出現する単語を用いて単語を定義するため、文(文章)が異なれば、単語ベクトルも異なります。
- 以下は"Obi-Wan, May the Force be with you."という文を用いて単語をベクトル化したものです。
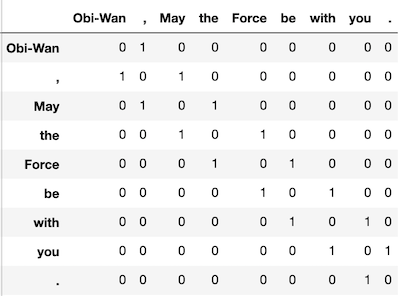
- 同じ単語が異なるベクトルであったり、まったく意味が違う単語が同じベクトルになってしまうので、これを避けるために多くの文(文章)を集めたコーパスを使用します。
2.3 共起行列の作成¶
- さて、これをやってみましょう。
- 対象テキストはリンカーンのゲティスバーグアドレスです。
Four score and seven years ago our fathers brought forth, upon this continent, a new nation, conceived in Liberty, and dedicated to the proposition that all men are created equal. Now we are engaged in a great civil war, testing whether that nation, or any nation so conceived, and so dedicated, can long endure. We are met on a great battle-field of that war. We have come to dedicate a portion of that field, as a final resting-place for those who here gave their lives, that that nation might live. It is altogether fitting and proper that we should do this. But, in a larger sense, we can not dedicate, we can not consecrate we can not hallow this ground. The brave men, living and dead, who struggled here, have consecrated it far above our poor power to add or detract. The world will little note, nor long remember what we say here, but it can never forget what they did here. It is for us, the living, rather, to be dedicated here to the unfinished work which they who fought here, have, thus far, so nobly advanced. It is rather for us to be here dedicated to the great task remaining before us that from these honored dead we take increased devotion to that cause for which they here gave the last full measure of devotion that we here highly resolve that these dead shall not have died in vain that this nation, under God, shall have a new birth of freedom and that government of the people, by the people, for the people, shall not perish from the earth.
# 対象テキスト
text = "Four score and seven years ago our fathers brought forth, upon this continent, a new nation, conceived in Liberty, and dedicated to the proposition that all men are created equal. Now we are engaged in a great civil war, testing whether that nation, or any nation so conceived, and so dedicated, can long endure. We are met on a great battle-field of that war. We have come to dedicate a portion of that field, as a final resting-place for those who here gave their lives, that that nation might live. It is altogether fitting and proper that we should do this. But, in a larger sense, we can not dedicate, we can not consecrate we can not hallow this ground. The brave men, living and dead, who struggled here, have consecrated it far above our poor power to add or detract. The world will little note, nor long remember what we say here, but it can never forget what they did here. It is for us, the living, rather, to be dedicated here to the unfinished work which they who fought here, have, thus far, so nobly advanced. It is rather for us to be here dedicated to the great task remaining before us that from these honored dead we take increased devotion to that cause for which they here gave the last full measure of devotion that we here highly resolve that these dead shall not have died in vain that this nation, under God, shall have a new birth of freedom and that government of the people, by the people, for the people, shall not perish from the earth."
# 使用するパッケージ
from nltk import word_tokenize
import numpy as np
# 単語分割
words = word_tokenize(text.lower())
# 単語にidをふって辞書を作る
# idがkeyでwordがvalueのディクショナリ
# wordがkeyでidがvalueのディクショナリ
word_to_id = {}
id_to_word = {}
# 単語分割したテキストからword_to_id, id_to_wordを作成する
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
# テキストをidに置き換える
corpus = [word_to_id[w] for w in words]
corpus = np.array(corpus)
corpus
array([ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,
13, 10, 14, 15, 16, 10, 17, 18, 19, 10, 2, 20, 21,
22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 27, 33,
18, 14, 34, 35, 36, 10, 37, 38, 24, 16, 10, 39, 40,
16, 41, 17, 10, 2, 41, 20, 10, 42, 43, 44, 30, 32,
27, 45, 46, 14, 34, 47, 48, 24, 36, 30, 32, 49, 50,
21, 51, 14, 52, 48, 24, 53, 10, 54, 14, 55, 56, 57,
58, 59, 60, 61, 62, 63, 10, 24, 24, 16, 64, 65, 30,
66, 67, 68, 69, 2, 70, 24, 32, 71, 72, 12, 30, 73,
10, 18, 14, 74, 75, 10, 32, 42, 76, 51, 10, 32, 42,
76, 77, 32, 42, 76, 78, 12, 79, 30, 22, 80, 26, 10,
81, 2, 82, 10, 59, 83, 60, 10, 49, 84, 66, 85, 86,
6, 87, 88, 21, 89, 39, 90, 30, 22, 91, 92, 93, 94,
10, 95, 43, 96, 97, 32, 98, 60, 10, 73, 66, 42, 99,
100, 97, 101, 102, 60, 30, 66, 67, 57, 103, 10, 22, 81,
10, 104, 10, 21, 105, 20, 60, 21, 22, 106, 107, 108, 101,
59, 109, 60, 10, 49, 10, 110, 85, 10, 41, 111, 112, 30,
66, 67, 104, 57, 103, 21, 105, 60, 20, 21, 22, 34, 113,
114, 115, 103, 24, 116, 117, 118, 82, 32, 119, 120, 121, 21,
24, 122, 57, 108, 101, 60, 61, 22, 123, 124, 125, 48, 121,
24, 32, 60, 126, 127, 24, 117, 82, 128, 76, 49, 129, 18,
130, 24, 12, 16, 10, 131, 132, 10, 128, 49, 14, 15, 133,
48, 134, 2, 24, 135, 48, 22, 136, 10, 137, 22, 136, 10,
57, 22, 136, 10, 128, 76, 138, 116, 22, 139, 30])
# 総語数の取得
corpus_size = len(words)
# 単語の種類数(vocabulary size)の取得
vocab_size = len(word_to_id)
# 空の行列を準備
co_matrix = np.zeros((vocab_size,vocab_size),dtype=np.int32)
# 分散表現の取得
# ウィンドウサイズ
window_size = 1
for idx,word_id in enumerate(corpus):
for i in range(1,window_size + 1):
left_idx = idx - 1
right_idx = idx + 1
if left_idx >= 0:
left_word_id = corpus[left_idx]
co_matrix[word_id,left_word_id] += 1
if right_idx < corpus_size:
right_word_id = corpus[right_idx]
co_matrix[word_id,right_word_id] += 1
2.4 単語ベクトルへのアクセス¶
co_matrix[word_to_id["and"]]
array([0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,
0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 0, 0, 0, 0], dtype=int32)
練習問題 1¶
../samples/alice_all.txtを読み込み"alice"と"rabbit"の単語ベクトルを求めてみましょう。
2.5 単語の類似度¶
- 単語をベクトルとして表現すると、単語間の「意味」の類似度を計算することができる。
- 仮に2つの数値で単語を表現することができたら、その値に基づいてXY平面上に単語をプロットすることが可能である。
- そして、平面上の距離、2つの点がなす角をそれらの単語の類似度とみなすことができる。
- ここでは、以下のようにあ2つの単語の「距離」を測定するためにユークリッド距離、2つの単語がなす角を測定するためにコサイン類似度を採用する。
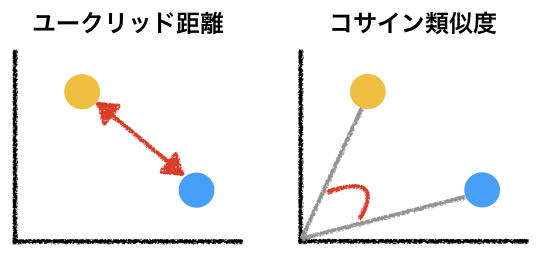
2.5.1 ユークリッド距離¶
- 「通常の」2点間の距離
- 点pと点qの距離は以下の式で求められる。
$$ d(p,q) = \sqrt{(q_1-p_1)^2 + (q_2-p_2)^2 + ... + (q_n -p_n)^2} \\ = \sqrt{\sum_{i=1}^n(q_i - p_i)^2} $$
2.5.2 コサイン類似度¶
- ベクトル同士の成す角度の近さを表す。
- 1に近ければ類似度が高く、0に近ければ類似度が低い。
- 2つのベクトル$\vec{p}=(p_1,p_2,...p_n)$および$\vec{q}=(q_1,q_2,...q_n)$に対して
- 以下の式で求められる。
$$ cos(\vec{p},\vec{q}) = \frac{p_1q_1 + p_2q_2 ... p_nq_n}{\sqrt{p_1^2+p_2^2+ ... p_n^2}\sqrt{q_1^2+q_2^2+...q_n^2}} \\ = \frac{\sum_{i=0}^np_nq_n}{\sqrt{\sum_{i=0}^np^2}\sqrt{\sum_{i=0}^nq^2}}$$
2.5.3 ユークリッド距離とコサイン類似度の計算¶
alice_all.txtでユークリッド距離とコサイン類似度を実際に求めてみよう。
# 対象テキストの取得
f = open("../samples/alice_all.txt","r")
raw_text = f.read()
f.close()
# 共起行列を作成する手順を関数にしてみました。
import numpy as np
from nltk import word_tokenize
def preprocess(text):
words = word_tokenize(text.lower())
word_to_id = {}
id_to_word = {}
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
corpus = [word_to_id[w] for w in words]
corpus = np.array(corpus)
return corpus,word_to_id,id_to_word
def create_co_matrix(corpus, vocab_size, window_size=1):
corpus_size = len(corpus)
co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)
for idx, word_id in enumerate(corpus):
for i in range(1, window_size + 1):
left_idx = idx - i
right_idx = idx + i
if left_idx >= 0:
left_word_id = corpus[left_idx]
co_matrix[word_id, left_word_id] += 1
if right_idx < corpus_size:
right_word_id = corpus[right_idx]
co_matrix[word_id, right_word_id] += 1
return co_matrix
# preprocessとcreat_co_matrix()を使って共起行列Vを作成
corpus,word_to_id,id_to_word = preprocess(raw_text)
vocab_size = len(word_to_id)
V = create_co_matrix(corpus,vocab_size)
- ユークリッド距離の計算
import numpy as np
# アリスとダイナの距離
np.linalg.norm(V[word_to_id["dinah"]] - V[word_to_id["alice"]])
208.62406380856453
# ダイナとウサギの距離
np.linalg.norm(V[word_to_id["dinah"]] - V[word_to_id["rabbit"]])
32.28002478313795
- コサイン類似度の計算
import scipy.spatial.distance as dis
# アリスとダイナの類似度
dis.cosine(V[word_to_id["dinah"]],V[word_to_id["alice"]])
0.4802880045984509
# ダイナとウサギの類似度
dis.cosine(V[word_to_id["dinah"]],V[word_to_id["rabbit"]])
0.7703758010851802
練習問題 2¶
上の例では直感に合うような結果はなかなか得られませんでした。その原因は以下であると仮定します。
- 対象としたコーパスのサイズが小さい。
- ユークリッド距離は単語の出現回数に影響を受けやすい。
この仮定に基づいて、コーパスサイズを大きくし(2016年のwikipediaから10000文)、類似度の計算にコサイン類似度を採用してみてください。このようにすると若干ですが、直感に合うような結果が得られるようになると思います。このデータは、2016年時点のwikipediaから10000文を抜粋したもので、文が改行で分けられ、個々の文に番号が振られ、アルファベット順に並んでいます。
# テキストの読み込み
f = open("../samples/eng_wikipedia_2016_10K-sentences.txt","r")
text = f.read()
import re
# テキストを改行で分ける。
text = text.split("\n")
# なぜか文の最後に数字の列(1942など)を登録してくれないので、
# 数字の列が最後にある文は削除
text2 = []
for i in text:
obj = re.search("¥d¥.$",i)
if not obj:
text2.append(i)
# 文番号を削除
text3 = []
for i in text2:
s,t = i.split("\t")
text3.append(t)
# 再度文字列に変換
text = " ".join(text2)
このデータを用いて、任意の単語の類似度を求めてみましょう。