学習者言語の分析（応用）1 （第1回）

  • 1.1 意味とは何か
  • 1.2 伝統的な意味論
  • 1.3 WordNet
  • 1.4 分布仮説と分散表現

1.1 意味とは何か¶

  • 言語学の一分野である意味論、あるいは、自然言語処理の一部で共有している問いのひとつとして「単語とは何か」という問いがある。

  • この問いは「意味とは何か」という問いと同じ意味を持つ場合がある。

1.2 伝統的な意味論¶

  • 単語の意味を「意味の成分」あるいは「意味の原子要素」へ分解するという手法を用いて単語を理解しようとした。
  • 以下では、4つの単語に対して4つの意味成分で表現した。
  • 当然ながらこれらの成分の組み合わせがそれぞれの単語を表現していると考えているわけではない。
[MALE] [FEMALE] [ADULT] [HUMAN] [MARRIED]
bachelor + − + + −
spinster − + + + −
woman − + + + n.a.
wife − + + + +
girl − + − + −
boy + − − + −

n.a.: not applicable (設定なし)

  • この「成分表」を用いることによって、ここにあげた単語の語彙的・意味的関係は明確になる。
    • "bachelor"と"spinster"は[MALE]および[FEMALE]成分のみが異なり、他の成分は同じということで対義関係であることが明示される。
  • このような方法は意味の「成分分析」と呼ばれる。
  • この成分分析が適用できる範囲は限られている。
    • 成分をいくつ用意すれば良いか分からない。
    • 単語が多義的である場合の表現方法が分からない。
    • 名詞以外の分析が難しい。
  • "sparrow"、"penguin"、"ostrich"の成分を考えた上で、"bird"の成分はどうなるであろうか。
  • "bachelor"は「学士」、「（若い）騎士」、「未婚男性」という意味があるが、"He became a bachelor in 2023."の"bachelor"は「学士」以外ありえないことを我々は知っているが成分分析を用いてどのように意味を特定することができるか。
  • 名詞でも色彩語は記述が困難。

実は、これ、認知心理学っぽい話で「カテゴリーは存在するか」という議論でもあったりする。例えば、動物を鳥と魚に分けることはできそうだけど、もっと分かりやすい例を言えば、1から100までの整数を偶数と奇数に分けることはできる。偶数のカテゴリに入るすべての整数は「2で割ると余りが0」という特徴を持っていて、奇数のカテゴリに入る全ての整数は「2で割ると余りが1」という特徴を持っている。では、「ゲーム」というカテゴリに入るものの特徴を言うことは可能でしょうか。それからプロトタイプ理論というものが出てきて...。家族的類似性とか。

  • で、単語の意味そのものを直接的に捉えようとすることはちょっとおいといて、単語同士の関係を考えることにした。
    • 「犬」と「ワンちゃん」、「わんわん」は類義語。
    • 「息子」、「娘」は「子ども」の下位語(hyponym)。
    • 「親」は「父」、「母」の上位語(hypernym)。
    • 「乗り物」の下に「車」、「バイク」、「自転車」があるみたいな。

1.3 WordNet¶

  • 上述の考え方に基づいて、単語の意味を表すために人手によって意味を定義することが考えられます。

  • 一般には、単語の定義を記述したものを集めた辞書を参照しますが、自然言語処理ではシソーラスという辞書が使われます。

  • シソーラスとは類義語辞書であり、意味が似ている単語が列挙されています。

  • ここでは、WordNetというシソーラス兼辞書を使用します。

  • 以下のようにimportします。

In [2]:
from nltk.corpus import wordnet as wn
  • 同義語は以下のように取得します。
  • studyには16個の意味が定義されています。
  • 出力は「見出し語」、「品詞」、「エントリ番号」の順になっています。
In [7]:
wn.synsets("dog")
Out[7]:
[Synset('dog.n.01'),
 Synset('frump.n.01'),
 Synset('dog.n.03'),
 Synset('cad.n.01'),
 Synset('frank.n.02'),
 Synset('pawl.n.01'),
 Synset('andiron.n.01'),
 Synset('chase.v.01')]
  • 定義は以下のように取り出せます。
In [8]:
dog = wn.synset("dog.n.01")
dog.definition()
Out[8]:
'a member of the genus Canis (probably descended from the common wolf) that has been domesticated by man since prehistoric times; occurs in many breeds'
  • 例文を見てみましょう。
In [9]:
dog.examples()[0]
Out[9]:
'the dog barked all night'
  • 同義語を見てみましょう。
In [10]:
dog.lemma_names()
Out[10]:
['dog', 'domestic_dog', 'Canis_familiaris']
  • 対応する日本語を見てみましょう。
In [11]:
wn.synset("dog.n.01").lemma_names("jpn")
Out[11]:
['イヌ', 'ドッグ', '洋犬', '犬', '飼い犬', '飼犬']
  • 上位語を見てみましょう。
In [12]:
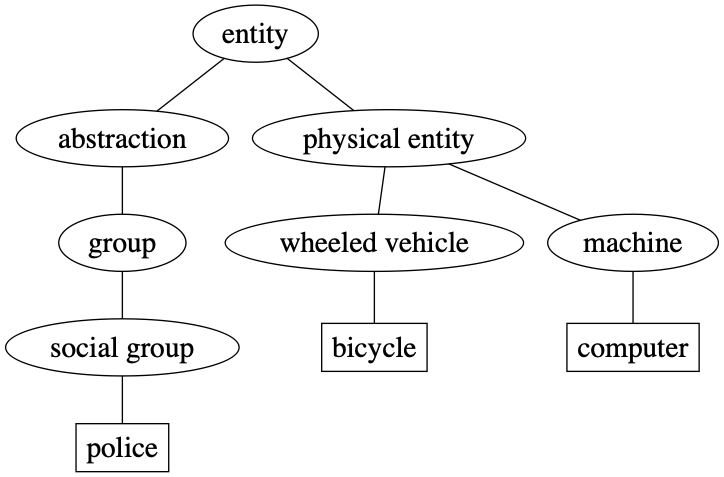
dog.hypernym_paths()
Out[12]:
[[Synset('entity.n.01'),
  Synset('physical_entity.n.01'),
  Synset('object.n.01'),
  Synset('whole.n.02'),
  Synset('living_thing.n.01'),
  Synset('organism.n.01'),
  Synset('animal.n.01'),
  Synset('chordate.n.01'),
  Synset('vertebrate.n.01'),
  Synset('mammal.n.01'),
  Synset('placental.n.01'),
  Synset('carnivore.n.01'),
  Synset('canine.n.02'),
  Synset('dog.n.01')],
 [Synset('entity.n.01'),
  Synset('physical_entity.n.01'),
  Synset('object.n.01'),
  Synset('whole.n.02'),
  Synset('living_thing.n.01'),
  Synset('organism.n.01'),
  Synset('animal.n.01'),
  Synset('domestic_animal.n.01'),
  Synset('dog.n.01')]]
  • Wordnetには単語が以下のように保存されていると考えることができます。

img01

  • このようにWordNetでは、類似度と包含関係により単語が分類されています。
  • この情報を利用して単語の類似度を計算することができます。
In [13]:
computer = wordnet.synset("computer.n.01")
bicycle = wordnet.synset("bicycle.n.01")
In [14]:
computer.path_similarity(dog)
Out[14]:
0.09090909090909091
In [15]:
computer.path_similarity(bicycle)
Out[15]:
0.14285714285714285
  • シソーラスの問題点として以下が指摘されている。
    • 人手のコストが膨大。
    • 時代によって単語同士の関係や単語そのものの意味が変わる。
    • 名詞以外のシソーラスを作るのが難しそう。
    • 微細な違いを表現することが難しそう。

1.4 分布仮説と分散表現¶

  • シソーラスの問題点を部分的に解決する方法。
  • 分布仮説とは「単語の意味は周囲の単語によって決まる」というアイディア。
  • 単語自体に意味はないという考え方。
  • "You shall know a word by the company it keeps!" -- J. R. Firth (1957).
  • 同じ文脈（コンテクスト）で出現する単語は同じ（ような）意味を持つ（ここでコンテクストとは「ある単語の周囲にある単語」という意味）。

それぞれの文におけるballの意味を考えてみましょう。

  1. The General ordered the cannons to be fired and the cannon balls breached the the barricade.
  2. The centre forward put the ball in the back of the net and the game was over.
  3. The ladies dressed for the ball that evening.

(奥村 (2010). 『自然言語処理の基礎』より)

  • 分布仮説を採用すると数学的なモデルが利用できる。

  • この、文脈に関する情報を用いて単語の意味を数量化するのが分散表現。

  • 分散表現とは単語を数値列（ベクトル）で表現する技術。

  • 分散表現をどのようにして得るのか実際にやってみよう。

  • 行の単語は名詞、列の単語は動詞である。

  • 数値は行の単語が列の単語の目的語（？）として出現する頻度である。

  • knifeは１列目の単語の目的語として51回出現したということである。

  • ???の単語は何でしょう？

  • 動詞は左から、get, see, use, hear, eat, kill

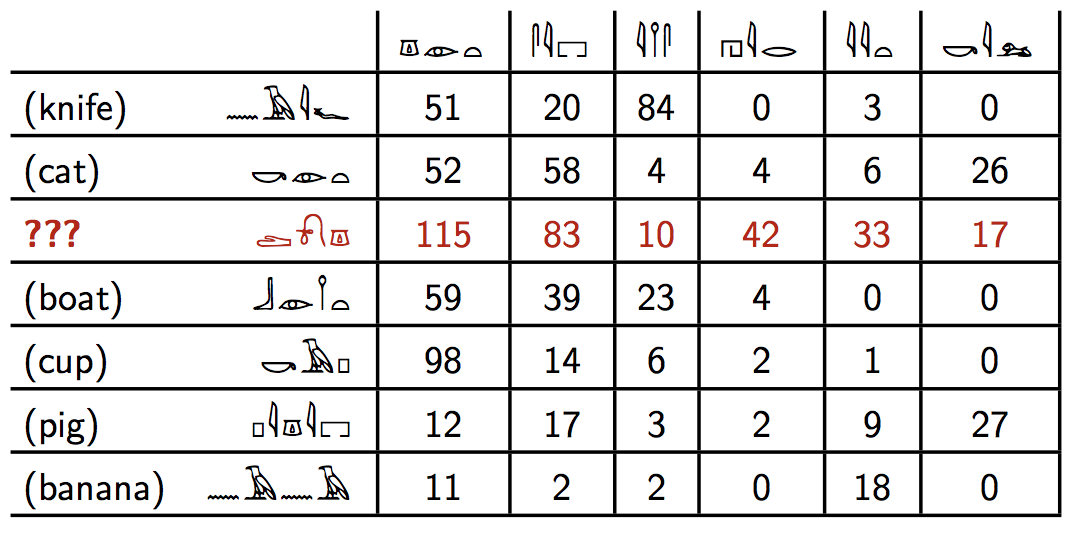
img01

Distributional Semantic Models Tutorial at NAACL-HLT 2010より抜粋

  • 実際にこの表をpythonで書いてみます。
In [1]:
import pandas as pd
import numpy as np

label = ["knife","cat","???","boat","cup","pig","banana"]
C = np.array([[51,20,84,0,3,0],
        [52,58,4,4,6,26],
       [115,83,10,42,33,17],
       [59,39,23,4,0,0],
       [98,14,6,2,1,0],
       [12,17,3,2,9,27],
       [11,2,2,0,18,0]])

C
Out[1]:
array([[ 51,  20,  84,   0,   3,   0],
       [ 52,  58,   4,   4,   6,  26],
       [115,  83,  10,  42,  33,  17],
       [ 59,  39,  23,   4,   0,   0],
       [ 98,  14,   6,   2,   1,   0],
       [ 12,  17,   3,   2,   9,  27],
       [ 11,   2,   2,   0,  18,   0]])
  • このままだと分かりにくいので、割合で示してみます（e.g. knifeとgetが共起した回数をknifeの全出現回数で割る）。
In [2]:
# Standardization
C2 = []
for c in C:
    sum_c = sum(c)
    D = []
    for c2 in c:
        D.append(c2/sum_c)
    C2.append(D)
  • これをpandasのDataFrameで出力してみます。
In [3]:
pd.options.display.precision = 3
table = pd.DataFrame({"knife":C2[0],"cat":C2[1],"???":C2[2],"boat":C2[3],"cup":C2[4],"pig":C2[5],"banana":C2[6]},index=["get","see","use","hear","eat","kill"])
Decipher_hieroglyphs = table.T
Decipher_hieroglyphs
Out[3]:
get see use hear eat kill
knife 0.323 0.127 0.532 0.000 0.019 0.000
cat 0.347 0.387 0.027 0.027 0.040 0.173
??? 0.383 0.277 0.033 0.140 0.110 0.057
boat 0.472 0.312 0.184 0.032 0.000 0.000
cup 0.810 0.116 0.050 0.017 0.008 0.000
pig 0.171 0.243 0.043 0.029 0.129 0.386
banana 0.333 0.061 0.061 0.000 0.545 0.000
  • この表から"???"と似ている振る舞いをしている単語を見つけてみましょう（正解はこのファイルの一番下にあります）。
  • より分かりやすくするためにPCA（主成分分析）という技術を用いて表現してみます。
In [4]:
from sklearn.decomposition import PCA

import matplotlib.pyplot as plt
%matplotlib inline

pca = PCA(n_components=2)
X = pca.fit_transform(C2)

plt.figure(figsize=(9,6))
for i in range(len(label)):
    plt.plot(X[:,0][i],X[:,1][i],"o",color="b")
    plt.annotate(label[i],xy=(X[:,0][i],X[:,1][i]),fontsize=22)
  • 正解は"dog"です。当たりましたか？