- 前回の授業では文の数や語数など作文の意味に関わらない特徴量を用いて評価を予測しました。
- 今回はBag-of-Wordsモデルに基づいて文章を単語ベクトルに変換したものを用いて評価を予測します。
3.1 ベイズの定理¶
- ナイーブベイズ分類器という機械学習の技法を用います。
- その前にベイズの定理を復習します。
3.1.0 確率、割合、面積¶
- 「確率とは何か」というところには深入りしない。
- この授業では、「過去のことを割合、未来のことを確率」ぐらいの感覚で。
- 2019年度から2023年度まででこの授業を履修した4年生以上の学生の割合は12%。
- 202X年度のこの授業に4年生以上の学生は12%の確率で含まれている。 $$ 割合 = 確率 $$
- 計算の時は割合も確率も平面の面積と考えると理解が進む場合がある。 $$ 割合 = 確率 = 面積 $$
- 高校までに言われてきた「同様に確からしい」というのは「経験的に同じ割合で起きてきた」ぐらいに考える。
3.1.1 条件付き確率¶
- ある事象(A)が起きる確率をP(A)と書く。
- Aが起きたことが分かってる場合にBが起きる確率をP(B|A)と書く。
- 数式による定義は $$P(B|A) = \frac{P(A\cap B)}{P(A)}$$
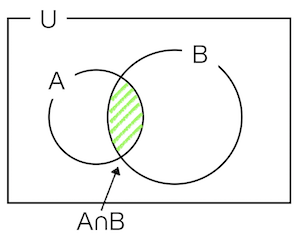
- $P(A\cap B)$はAとBが同時に起きる確率を示します。
- 以下の図で示すように、$P(B|A)$は、$P(A)$に占める$P(A\cap B)$の割合と考えることができます。
- サイコロで考えると、Aを「偶数の目がでる」、Bを「3より大きな目がでる」とすると、
- $ A \cap B$は「3より大きい偶数の目がでる」になる。
- サイコロの目の全事象は6で、偶数の目は2, 4, 6の3つ、3より大きな目は4, 5, 6。
- 確率は対象の事象の数を全事象の数で割ったもの。
- なので、$P(A)$は0.5(3/6)で、$ A \cap B$は0.33(2/6)なので、$P(B|A)$は0.66(0.33/0.5)になる。
- 以下で確かめてみよう。
import numpy as np
# サイコロを10000回振る。
U = []
for i in range(10000):
U.append(np.random.randint(1,7))
# 10000回振って出た目のうち、目が偶数のものの割合
A = []
for i in U:
if i % 2 == 0:
A.append(i)
P_A = len(A)/len(U)
P_A
0.4986
# 10000回振って出た目のうち、目が偶数かつ3以上のものの割合
A_B = []
for i in U:
if i % 2 == 0 and i > 3:
A_B.append(i)
P_A_B = len(A_B)/len(U)
P_A_B
0.3301
# P(B|A)の確率
BA = []
for i in A:
if i > 3:
BA.append(i)
P_BA = len(BA)/len(A)
P_BA
0.6620537505014039
3.1.2 例題1¶
ある夫婦には子どもが2人いる。2人のうち少なくとも1人は男の子であると分かったとき、2人とも男の子である確率を求めよ。男の子が生まれる確率、女の子が生まれる確率は共に1/2とする。求めたいのは
$$P(B|A) = \frac{P(A\cap B)}{P(A)}$$
であり、この$P(A\cap B)$と$P(A)$を何にするかを考える。 *「 男の子が生まれる確率、女の子が生まれる確率は共に1/2」だからと言って、答えは0.5ではない。
すべての組み合わせ(全事象)は男男、男女、女男、女女の4通り。
Aを「2人いる子どものうち少なくとも1人が男の子」という事象とする。
全事象のうちの3つ組み合わせに男が入っているので、Aは0.75(3/4)。
Bを「2人とも男の子」の事象とする。
$P(A\cap B)$は「2人いる子どものうち少なくとも男の子が1人は含まれている」と「2人とも男」なので0.25(1/4)。(つまり「2人とも男」)。
よって、1人の子どもが男の子だと分かったときに、2人とも男の子の確率$P(B|A)$は0.25/0.75 = 0.333..
以下で確かめてみよう。
# d1とd2は同じ確率で1か0が出る。
# 1だったらM(男)、2だったらF(女)とする。
C = []
for i in range(10000):
d1 = np.random.randint(2)
d2 = np.random.randint(2)
if d1 == 0:
c1 = "M"
else:
c1 = "F"
if d2 == 0:
c2 = "M"
else:
c2 = "F"
C.append([c1,c2])
- Cは10000組の子どもの組。
- このうちどちらか一方がM(男)である組をAに保存する。
A = []
for i in C:
if "M" in i:
A.append(i)
P_A = len(A)/len(C)
P_A
0.7449
- Aの組数をCの組数で割って$P(A)$を求めた。
- 以下では、両方ともM(男)である組をCから取り出してA_Bに保存する。
A_B = []
for i in C:
if "M" in i and i == ["M","M"]:
A_B.append(i)
P_A_B = len(A_B) / len(C)
P_A_B
0.2485
- 求めた両方ともM(男)である組数を総数(C)で割って$P (A \cap B)$を求めた。
- $ P(B|A) = 0.25 \div 0.75 $で0.33。
- どちらか一方がM(男)の組(A)の数で両方とも男(M)の組(BA)の数を割ると0.33。
BA = []
for i in A:
if i == ["M","M"]:
BA.append(i)
P_BA = len(BA)/len(A)
P_BA
0.3336018257484226
3.1.3 例題2¶
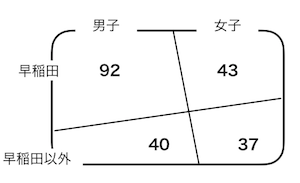
あるサークルの構成員の数は212人で、男子132人、女子80人。早稲田の学生は135人、早稲田以外の学生は77人である。知らない男子がサークルの部室にいたとき、この男子が早稲田の学生である確率は?
3.1.4 ベイズの定理¶
条件付き確率の式(1)
(1) $$P(B | A) = \frac{P(A\cap B)}{P(A)}$$
の両辺にP(A)をかけると(2)
(2) $$P(A)P(B|A) = P(A\cap B)$$
今度はBが起きたと分かってる時の場合(3)
(3) $$P(A|B) = \frac{P(A\cap B)}{P(B)}$$
(3)の両辺にP(B)をかけると(4)
(4) $$P(B)P(A|B) = P(A\cap B)$$
まさかの(5)
(5) $$P(B)P(A|B) = P(A)P(B|A)$$
でこれの両辺をP(B)で割ると(6) これがベイズの定理。
(6) $$P(A|B) = \frac{P(A)P(B|A)}{P(B)}$$
3.1.5 自動採点におけるベイズの定理の利用¶
自動採点の文脈でベイズの定理(7)
$$P(評価|作文) = \frac{P(評価)P(作文|評価)}{P(作文)}$$
例えば、評価が良い/悪いの2段階だった場合、以下の大小関係を比較して評価を決定する。(8,9)
$$P(良い|作文) = \frac{P(良い)P(作文|良い)}{P(作文)} $$
$$P(悪い|作文) = \frac{P(悪い)P(作文|悪い)}{P(作文)} $$
分母のP(作文)は共通なので、大小比較には関係ないので削除する。(10,11)
$$P(良い|作文)\propto P(良い)P(作文|良い) $$
$$P(悪い|作文)\propto P(悪い)P(作文|悪い) $$
例えば、100人が作文を書いて「良い」評価を受けた受験者が40人で、「悪い」評価を受けた受験者が60人であった場合、$P(良い)$は0.4、$P(悪い)$は0.6(それぞれ40/100、60/100)。
$P(作文|良い)$と$P(作文|悪い)$をどうするかが難しい。
ここで、神様しか知らない単語リストが存在して、サイコロを振り、出た目によってそのリストから単語を抜き出して個々の学習者の作文ができあがると仮定する。単語ごとにサイコロを振るので、100語の作文を作成するためには100回サイコロを振る。この考え方がナイーブなのでこの手法がナイーブベイズと呼ばれている。
さらに単純化して、神様しか知らない単語リストには3種類の単語が掲載されていて、作文の特徴量として、この3語の頻度のみに注目することにする。$w_1, w_2, w_3$をこれらの単語の頻度とする。「良い」のカテゴリでは$P(w_1) = 0.5, P(w_2) = 0.3, P(w_3) = 0.2$ 、「悪い」のカテゴリでは$P(w_1) = 0.2, P(w_2) = 0.3, P(w_3) = 0.5$とする。これは、多項分布という確率分布に従うことが知られていて以下の式で表される。
ただし、$p_1^{w_1} + p_2^{w_2} + p_3^{w_3} = 1$、$w_1 + w_2 + w_3 = w$である。
$$ P(w_1, w_2, w_3) = \frac{w!}{w_1! w_2! w_3!}p_1^{w_1} p_2^{w_2} p_3^{w_3}$$
例えば、$w_1$が3回、$w_2$が1回、$w_3$が1回出現した作文が「良い」という評価の作文として得られる確率は
$$ P(w_1=3, w_2=1, w_3=2) = \frac{6!}{3! \times 1! \times 2!} \times 0.5^3 \times 0.3^1 \times 0.2^2 = 0.09$$
また、この作文が「悪い」という評価の作文として得られる確率は
$$ P(w_1=3, w_2=1, w_3=2) = \frac{6!}{3! \times 1! \times 2!} \times 0.2^3 \times 0.3^1 \times 0.5^2 = 0.036$$
P(作文|良い)、P(作文|悪い)が得られたので、それぞれにP(良い)とP(悪い)をかけて、
$$P(良い) = 0.09 \times 0.4 = 0.036 $$
$$P(悪い) = 0.036 \times 0.6 = 0.021$$
となるので、この作文の評価は「良い」となる。
3.2 ナイーブベイズ分類器の実装¶
- 前回の授業で利用した英語学習者と英語母語話者の作文を用いて、これらの作文の2-gramを特徴量としてナイーブベイズ分類器を用いて分類する。
3.2.1 準備¶
import os
# データの取得Y = [0] * len(Feature_NNS) + [1] * len(Feature_NS)
fname_NS = os.listdir("../DATA02/NICE_NS/")
T_NS = []
for i in fname_NS:
f = open("../DATA02/NICE_NS/"+i,"r")
text = f.read()
f.close()
T_NS.append(text)
fname_NNS = os.listdir("../DATA02/NICE_NNS/")
T_NNS = []
for i in fname_NNS:
f = open("../DATA02/NICE_NNS/"+i,"r")
text = f.read()
f.close()
T_NNS.append(text)
# テキストの結合
X_text = T_NNS + T_NS
# 正解ラベルの作成
Y = [0] * len(T_NNS) + [1] * len(T_NS)
3.2.2 データの分割とベクトル化¶
- 作文をベクトル化する際に、全体でベクトル化するとテストデータに出てくる単語をカンニングすることになるので、テストデータと学習データに分割した後にベクトル化する。
# データの分割
from sklearn.model_selection import train_test_split
X_text_train,X_text_test,y_train,y_test = train_test_split(X_text,Y,test_size=0.2)
# 作文のベクトル化
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(min_df=1,ngram_range=(2,2))
vectorizer.fit(X_text_train)
X_train = vectorizer.transform(X_text_train).toarray()
X_test = vectorizer.transform(X_text_test).toarray()
3.2.3 ナイーブベイズ分類器による予測精度の検証¶
# ナイーブベイズ分類器のクラス
from sklearn.naive_bayes import MultinomialNB
# インスタンスの生成
nbc = MultinomialNB()
# トレーニングデータでモデル構築
nbc.fit(X_train,y_train)
# テストデータの評価を予測して、予測精度の出力
nbc.score(X_test,y_test)
0.972972972972973
3.2.4 交差検証¶
S = []
vectorizer = CountVectorizer(min_df=1,ngram_range=(2,2))
nbc = MultinomialNB()
for i in range(10):
X_text_train,X_text_test,y_train,y_test = train_test_split(X_text,Y,test_size=0.2)
vectorizer.fit(X_text_train)
X_train = vectorizer.transform(X_text_train).toarray()
X_test = vectorizer.transform(X_text_test).toarray()
nbc.fit(X_train,y_train)
S.append(nbc.score(X_test,y_test))
np.average(S)
0.963963963963964
3.2.5 混同行列¶
from sklearn.metrics import confusion_matrix
X_text_train,X_text_test,y_train,y_test = train_test_split(X_text,Y,test_size=0.2)
vectorizer.fit(X_text_train)
X_train = vectorizer.transform(X_text_train).toarray()
X_test = vectorizer.transform(X_text_test).toarray()
nbc = MultinomialNB()
nbc.fit(X_train,y_train)
Y_pred = nbc.predict(X_test)
cm = confusion_matrix(y_test,Y_pred)
cm
array([[71, 2],
[ 4, 34]])
import seaborn as sns
sns.heatmap(cm,annot=True,cmap="Blues")
<AxesSubplot: >
練習問題1¶
ここまで扱ってきたデータの英語学習者に関して部分的に評価値が付与されています。評価値は"../DATA02/nice_evaluation.csv"に保存されています。評価された作文は"../DATA02/NICE_NNS2"に保存されています。ここで学んだ同様の手順でこのデータを自動採点するシステムを構築し、交差検証を行いなさい。
練習問題2¶
前回の練習問題同様、文数、語数、type token ratio、words per sentenceを予測変数として、ナイーブベイズ分類器を用いて評価値を予測する自動採点システムを構築し、交差検証を行いなさい。
from nltk import word_tokenize,sent_tokenize
def counters(X):
s = len(sent_tokenize(X))
tokens = word_tokenize(X)
w = len(tokens)
types = len(list(set(tokens)))
ttr = types / w
wps = w / s
Y = [s,w,ttr,wps]
return Y
確率分布について授業で扱っていないのですが、この場合のナイーブベイズ分類器は以下のようにGaussianNBを利用してください。
# 以下のようにimportしてください。
from sklearn.naive_bayes import GaussianNB
例題2の解答¶
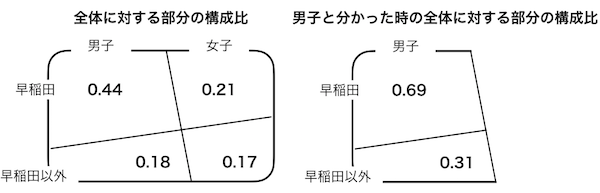
- $P(A)$を男子である確率、$P(B)$を早稲田の学生である確率、$P(A \cap B)$を男子で早稲田の学生である確率、$P(B|A)$を男子学生だと分かったときに早稲田の学生である確率とする。
- $P(A)$は0.62(132/212)、$P(A \cap B)$は0.43(92/212)
- よって、$P(B|A)$は0.69(0.43/0.62)
$$P(B|A) = \frac{P(A\cap B)}{P(A)}$$