学習者言語の分析（基礎）2（第2回）

  • 2.1 使用するデータの準備
  • 2.2 k-近傍法の概要
  • 2.3 k-近傍法の実装
  • 2.4 交差検証
  • 2.5 混同行列
  • 練習問題
  • 実際の学習者言語のデータを用いて、機械学習をPythonで実装します。
  • 機械学習の技法は、学習と予測の2つのプロセスを分けて捉えると理解が容易です。

2.1 使用するデータの準備¶

  • 英語学習者と英語母語話者が書いた作文を用います。
In [1]:
# 使用するパッケージ
import os
from nltk import word_tokenize,sent_tokenize
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
%matplotlib inline
from sklearn.metrics import confusion_matrix
import seaborn as sns
In [2]:
fname_NS = os.listdir("../DATA02/NICE_NS/")

T_NS = []

for i in fname_NS:
    f = open("../DATA02/NICE_NS/"+i,"r")
    text = f.read()
    f.close()
    T_NS.append(text)
In [3]:
fname_NNS = os.listdir("../DATA02/NICE_NNS/")

T_NNS = []

for i in fname_NNS:
    f = open("../DATA02/NICE_NNS/"+i,"r")
    text = f.read()
    f.close()
    T_NNS.append(text)
  • 以下の関数ではそれぞれのテキストから以下の特徴量を抽出します。
    • 総文数
    • 総語数
    • Type token ratio (異なり語の割合)
    • 1文あたりの平均語数
  • 今回はこの特徴量を用いて機械学習のプロセスを学びます。
In [4]:
def feature_count(X):
    s = len(sent_tokenize(X))
    tokens = word_tokenize(X)
    w = len(tokens)
    types = len(list(set(tokens)))
    ttr = types / w
    wps = w / s
    Y = [s,w,ttr,wps]
    return Y
  • feature_count()を用いてそれぞれのテキストから特徴量を抽出します。
In [5]:
Feature_NS =[]

for i in T_NS:
    j = feature_count(i)
    Feature_NS.append(j)
    
Feature_NNS =[]

for i in T_NNS:
    j = feature_count(i)
    Feature_NNS.append(j)
In [6]:
# データの結合
X = Feature_NNS + Feature_NS
Y = [0] * len(Feature_NNS) + [1] * len(Feature_NS)
  • 前回の授業では交差検証を自分で行いましたが、今後は以下のパッケージを使用します。
  • train_test_splitを用いると特徴量とラベルをランダムに学習データとテストデータに分けてくれます。
In [7]:
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2) # test_sizeでテストデータの割合を指定する
  • ここまででデータの準備が終了しました。

2.2 k-近傍法の概要¶

  • 前回の授業で扱った「最も簡単な自動採点」の手順とかなり似ています。
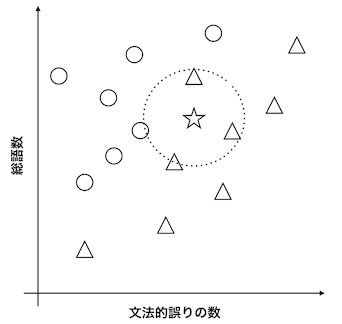
  • 以下の図で、△と○は異なるクラスのデータで、文法的誤りの数と総語数という2つの特徴量でプロットされています。
  • 「学習」という言葉が持つイメージとは少し異なりますが、k-近傍法では、複数のクラスを複数の特徴量でプロットすることが「学習」のプロセスにあたります。
  • 「予測」のプロセスでは、クラスが不明なデータ（図では☆で示されています）をプロットし、この☆から距離が近いk個のクラス(図ではk=4)をカウントし、多い方のクラスを☆のクラスとします。 fig01

2.3 k-近傍法の実装¶

  • 上で整形したデータを用いて英語学習者と英語母語話者を弁別するシステムを構築します。
In [8]:
# パッケージのimport
from sklearn.neighbors import KNeighborsClassifier

# インスタンスの生成
# n_neighborsでkの値を指定
knn = KNeighborsClassifier(n_neighbors=3)

# 学習
knn.fit(X_train,Y_train)

# 予測
Y_pred = knn.predict(X_test)

# 精度
knn.score(X_test,Y_test)
Out[8]:
0.8468468468468469
  • kを変化させた時の予測精度
In [9]:
N = []
S = []

for i in range(1,31):
    knn = KNeighborsClassifier(n_neighbors=i)
    knn.fit(X_train,Y_train)
    score = knn.score(X_test,Y_test)
    N.append(i)
    S.append(score)

plt.xlabel("number_of_k")
plt.ylabel("accuracy")
plt.plot(N,S)
Out[9]:
[<matplotlib.lines.Line2D at 0x177456b20>]
No description has been provided for this image

2.4 交差検証¶

In [10]:
S = []
for i in range(1,11):
    X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)
    knn = KNeighborsClassifier(n_neighbors=10)
    knn.fit(X_train,Y_train)
    S.append(knn.score(X_test,Y_test))
In [11]:
import numpy as np
np.average(S)
Out[11]:
0.8963963963963965

2.5 混同行列¶

  • 予測精度を検討するために予測ラベルと本当のラベルを可視化して表現します。
In [12]:
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2)

knn = KNeighborsClassifier(n_neighbors=10)
knn.fit(X_train,Y_train)
Y_pred = knn.predict(X_test)
In [13]:
cm = confusion_matrix(Y_test,Y_pred)
cm
Out[13]:
array([[63,  9],
       [ 6, 33]])
In [14]:
sns.heatmap(cm,annot=True,cmap="Blues")
Out[14]:
<AxesSubplot: >
No description has been provided for this image

練習問題¶

ここまで扱ってきたデータの英語学習者に関して部分的に評価値が付与されています。評価値は"../DATA02/nice_evaluation.csv"に保存されています。評価された作文は"../DATA02/NICE_NNS2"に保存されています。ここで学んだ同様の手順でこのデータを自動採点するシステムを構築し、交差検証を行いなさい。