学習者言語の分析（基礎）1 第6回

• 6.1 特徴量スケーリング（正規化と標準化）
  • 6.1.2 正規化
  • 6.1.3 標準化

6.1 特徴量スケーリング（正規化と標準化）

• 以下の図Aでは、2つ変数で3つのグループを明確に分類することができそうです。
• 一方で、図Bでは、□と△のグループを2つの変数で分類することは難しそうです。

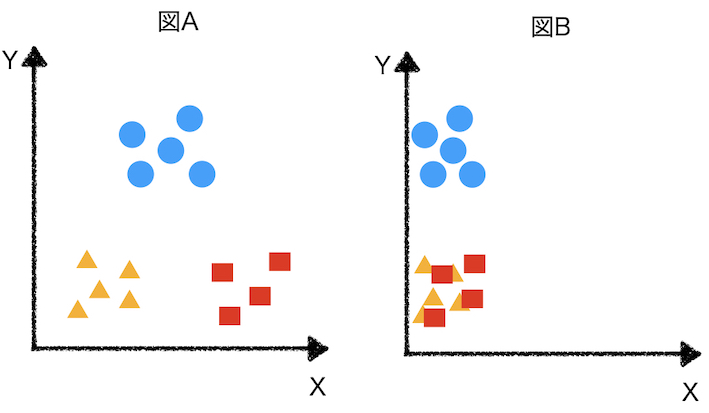
• 図Bの変数Yは100から10000までの値をとるが、図Bの変数Xは0から100までの値しかとらないことが原因で分類ができなくなっているかもしれません。
• 変数の取りうる値の幅によって、ユークリッド距離、コサイン類似度の計算結果が異なる場合があります。
• 特徴量スケーリングを行うことによって、この問題を解決することが可能な場合があります。

6.1.2 正規化

• 正規化にはさまざまな手法がありますが、ここでは最も簡単なMin-Max Normalization（最少・最大正規化）を取り上げます。
• Min-Max Normalizationは以下の手順で行われます。

$$ x_{norm} = \frac{x - min(X)}{max(X) - min(X)} $$

• $ x_{norm}$（正規化された$x$）は、最大値$max(X)$と最小値$min(X)$の幅の中で、最小値からどれぐらい離れているかという割合のような値に変換します。
• ここで、$x_{norm}$の最小値は0、最大値は1に変換されます。

import numpy as np

# 乱数の生成
X = np.random.randint(1,100,100)
Y = np.random.randint(1,100000,100)

import pandas as pd

# データフレームに保存
data = pd.DataFrame({"X":X,"Y":Y})
data.head()

	X	Y
0	17	16544
1	66	70736
2	63	60201
3	92	35504
4	79	56038

import matplotlib.pyplot as plt
%matplotlib inline

# 散布図
data.plot(kind="scatter",x="X",y="Y")
plt.xlim(0,10000)

(0.0, 10000.0)

# X, Yの最小値、最大値
X_min = data.min()[0]
X_max = data.max()[0]
Y_min = data.min()[1]
Y_max = data.max()[1]

# Xの正規化
data["X_n"] = (data["X"] - X_min) / (X_max - X_min)
# Yの正規化
data["Y_n"] = (data["Y"] - Y_min) / (Y_max - Y_min)

data.head()

	X	Y	X_n	Y_n
0	17	16544	0.163265	0.164090
1	66	70736	0.663265	0.707766
2	63	60201	0.632653	0.602075
3	92	35504	0.928571	0.354304
4	79	56038	0.795918	0.560310

data.describe()

	X	Y	X_n	Y_n
count	100.000000	100.000000	100.000000	100.000000
mean	51.780000	49201.500000	0.518163	0.491723
std	28.058949	29768.264775	0.286316	0.298647
min	1.000000	188.000000	0.000000	0.000000
25%	31.250000	24764.750000	0.308673	0.246564
50%	52.500000	54084.500000	0.525510	0.540711
75%	72.500000	73537.500000	0.729592	0.735872
max	99.000000	99865.000000	1.000000	1.000000

data.plot(kind="scatter",x="X_n",y="Y_n")

<AxesSubplot:xlabel='X_n', ylabel='Y_n'>

6.1.3 標準化

• 標準化は以下の手順で行われます。

$$ x_{std} = \frac{x - \bar{x}}{\sigma} $$

• 上の式において、$\bar{x}$は、データの平均値（算術平均）、$\sigma$は標準偏差。
• （標本）標準偏差は以下で定義される、個々のデータが平均値からどれぐらい離れているかの平均値。

$$ \sigma = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_{i} - \bar{x})} $$

• 標準化された値は、平均が0、標準偏差が1になる。

# X, Yの平均値
X_mean = data["X"].mean()
X_std = data["X"].std()
Y_mean = data["Y"].mean()
Y_std = data["Y"].std()

# Xの標準化
data["X_s"] = (data["X"] - X_mean) / X_std

# Yの標準化
data["Y_s"] = (data["Y"] - Y_mean) / Y_std

data.head()

	X	Y	X_n	Y_n	X_s	Y_s
0	17	16544	0.163265	0.164090	-1.239533	-1.097058
1	66	70736	0.663265	0.707766	0.506790	0.723405
2	63	60201	0.632653	0.602075	0.399872	0.369504
3	92	35504	0.928571	0.354304	1.433411	-0.460138
4	79	56038	0.795918	0.560310	0.970100	0.229657

data.describe()

	X	Y	X_n	Y_n	X_s	Y_s
count	100.00	100.00	100.00	100.00	1.00e+02	1.00e+02
mean	51.78	49201.50	0.52	0.49	-1.50e-17	1.55e-17
std	28.06	29768.26	0.29	0.30	1.00e+00	1.00e+00
min	1.00	188.00	0.00	0.00	-1.81e+00	-1.65e+00
25%	31.25	24764.75	0.31	0.25	-7.32e-01	-8.21e-01
50%	52.50	54084.50	0.53	0.54	2.57e-02	1.64e-01
75%	72.50	73537.50	0.73	0.74	7.38e-01	8.18e-01
max	99.00	99865.00	1.00	1.00	1.68e+00	1.70e+00

data.plot(kind="scatter",x="X_s",y="Y_s")

<AxesSubplot:xlabel='X_s', ylabel='Y_s'>

• データによっては、標準化、正規化によって同じような値が得られる時もあるし、そうでない時もある。
• 正規化、標準化は、常に行えば良いというものではない。
• 結果によって判断する。

演習問題

• ../DATA01/text_train/には学習者の作文が保存されています。
• これらの作文に対する評価は../DATA02/eva_train.csvに保存されています。
• 評価はGood=1、Poor=0のように2値で付与されています。
• このデータを用いて自動採点システムを構築し、../DATA01/text_test/に保存されている作文を評価します。
• 評価に関して以下ような予想をし、これを前提に自動採点システムを構築します。
  • 評価が高い作文には複雑な文が含まれている→文の平均語数が多い
  • 評価が高い作文には難しい（頻度が低い）単語が含まれている→単語の平均文字数が多い
  • 評価が高い作文にはさまざまな単語が含まれている→TTRの値が大きい
• また、特徴量の値が近いと同じ評価を受けると考えます。