学習者言語の分析(基礎)第5回 2
- 文(文章)を数値で表現することによって、テキストの分類などに役立つときがあります。
- ここでは、文(文章)の数値表現と文(文章)同士の類似度の計算方法を学びます。
5.4 Bag-of-words¶
- テキストデータを数値として表現する方法としてBag-of-Words (BoW)というアプローチがあります。
In [1]:
# 例文
a = "I walk to school"
b = "I walked to school"
c = "Yesterday I walked to school"
d = "I walked to school yesterday"
- 上の例文をBoWで表現すると以下のようになります。
- 単語の出現回数を数えて数値の列(ベクトル)として扱います(1文字の単語はカウントしない)。
- BoWは単語の出現順序を考慮していません。
| 単語 | 文a | 文b | 文c | 文d |
|---|---|---|---|---|
| school | 1 | 1 | 1 | 1 |
| to | 1 | 1 | 1 | 1 |
| walk | 1 | 0 | 0 | 0 |
| walked | 0 | 1 | 1 | 1 |
| yesterday | 0 | 0 | 1 | 1 |
- 以下ではsklearnというパッケージのCountVectorizerというクラスを用いて例文をBoWで表現しています。
In [2]:
# 対象となる文をリストに格納する。
L = [a,b,c,d]
# sklearnのクラスのインポート
from sklearn.feature_extraction.text import CountVectorizer
# インスタンスの作成
# 引数の"mind_df=1"は「1回以上出現した単語を数える」という意味
# 2回以上出現した単語だけをカウントするには"min_df=2"とする
vectorizer = CountVectorizer(min_df=1)
In [3]:
# カウントする単語を登録(インスタンスにデータを保存している)
vectorizer.fit(L)
# 文のベクトル表現を算出 (Compressed Sparse Row)
X = vectorizer.transform(L)
# 行列の出力(上の表とは行と列が入れ替わっている)
X.toarray()
Out[3]:
array([[1, 1, 1, 0, 0],
[1, 1, 0, 1, 0],
[1, 1, 0, 1, 1],
[1, 1, 0, 1, 1]])
In [4]:
# 表1と同じにしたかったら
X.toarray().transpose()
Out[4]:
array([[1, 1, 1, 1],
[1, 1, 1, 1],
[1, 0, 0, 0],
[0, 1, 1, 1],
[0, 0, 1, 1]])
In [5]:
# 新たな文を同じ方法でベクトル化する
M = ["I yesterday walked to school"]
X2 = vectorizer.transform(M).toarray()
X2
Out[5]:
array([[1, 1, 0, 1, 1]])
- 単語のみのBag of wordsだと単語の出現順序を捉えることができない。
- "He stole a car, and I bought a banana."と"I stole a car, and he bought a banana."は同じになってしまう。
5.5 N-gram¶
- 隣り合うN個のかたまりのこと
- "This is a pen"の2-gramは["this is", "is a", "a pen"]
- 1-gramはuni-gram、2-gramはbi-gram、3-gramはtri-gram、それ以降はfour-gramみたいに読む。
- N-gramを使うと多少語順を考慮できる。
- 上で求めた数値列は1-gramである。
- 以下ではCountVectorizerでbigramを求めている。
In [6]:
L = [a,b,c,d]
# "ngram_range=(X,Y)"で求めるN-gramを指定する。
# 「XからY」までという意味
# uni-gram, bi-gram, tri-gramの3つを求めたい場合は"ngram_range=(1,3)とする
bigram_vectorizer = CountVectorizer(min_df=1,ngram_range=(2,2))
bigram_vectorizer.fit(L)
X_b = bigram_vectorizer.transform(L).toarray()
X_b
Out[6]:
array([[0, 1, 1, 0, 0],
[0, 1, 0, 1, 0],
[0, 1, 0, 1, 1],
[1, 1, 0, 1, 0]])
In [7]:
# 以下のメソッドでbigramのリストが得られる
bigram_vectorizer.get_feature_names()
/Users/yusukekondo/Library/Python/3.9/lib/python/site-packages/sklearn/utils/deprecation.py:87: FutureWarning: Function get_feature_names is deprecated; get_feature_names is deprecated in 1.0 and will be removed in 1.2. Please use get_feature_names_out instead. warnings.warn(msg, category=FutureWarning)
Out[7]:
['school yesterday', 'to school', 'walk to', 'walked to', 'yesterday walked']
5.6 文(文章)の類似度¶
- このように文を数値列(ベクトル)として表現するとユークリッド距離やコサイン類似度を計算できる。
- 仮に文が2つの数値の列で表現できるとした場合、その値に基づいてXY平面上にプロットすることが可能である。
- そして、平面上の距離、2つの点がなす角を文同士の類似度と見なすことができる。
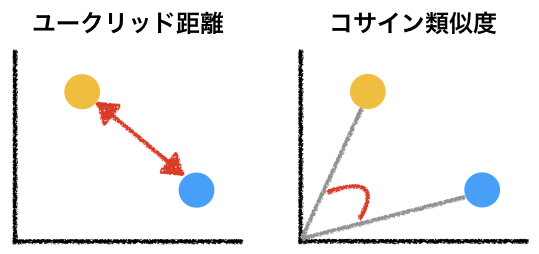
- 2つのベクトルの距離を測るのがユークリッド距離
- 2つのベクトルの角度を測るのがコサイン類似度
5.6.1 ユークリッド距離¶
「通常の」2点間の距離
点pと点qの距離は以下の式で求められる。 $$ d(p,q) = \sqrt{(q_1-p_1)^2 + (q_2-p_2)^2 + ... + (q_n -p_n)^2} \\ = \sqrt{\sum_{i=1}^n(q_i - p_i)^2} $$
表1の場合、文が5つの単語で表現されているので、
5次元空間におけるユークリッド距離を求める。
In [8]:
# X.toarray()を代入
X_a = X.toarray()
# numpyのインポート
import numpy as np
# ユークリッド距離を求める
np.linalg.norm(X_a[2] - X_a[3])
Out[8]:
0.0
In [9]:
# すべての文間の類似度を求める
X_euc = []
for i in X_a:
x = []
for j in X_a:
x.append(np.linalg.norm(i - j))
X_euc.append(x)
X_euc
Out[9]:
[[0.0, 1.4142135623730951, 1.7320508075688772, 1.7320508075688772], [1.4142135623730951, 0.0, 1.0, 1.0], [1.7320508075688772, 1.0, 0.0, 0.0], [1.7320508075688772, 1.0, 0.0, 0.0]]
In [15]:
import pandas as pd
# 2桁のみ表示
pd.options.display.precision = 2
# データフレームで表示
df2 = pd.DataFrame({"a":X_euc[0],
"b":X_euc[1],
"c":X_euc[2],
"d":X_euc[3]},
index=["a","b","c","d"])
df2
Out[15]:
| a | b | c | d | |
|---|---|---|---|---|
| a | 0.00 | 1.41 | 1.73 | 1.73 |
| b | 1.41 | 0.00 | 1.00 | 1.00 |
| c | 1.73 | 1.00 | 0.00 | 0.00 |
| d | 1.73 | 1.00 | 0.00 | 0.00 |
5.6.2 コサイン類似度¶
- ベクトル同士の成す角度の近さを表す。
- 1に近ければ類似度が高く、0に近ければ類似度が低い。
- 2つのベクトル$\vec{p}=(p_1,p_2,...p_n)$および$\vec{q}=(q_1,q_2,...q_n)$に対して
- 以下の式で求められる。 $$ cos(\vec{p},\vec{q}) = \frac{p_1q_1 + p_2q_2 ... p_nq_n}{\sqrt{p_1^2+p_2^2+ ... p_n^2}\sqrt{q_1^2+q_2^2+...q_n^2}} \\ = \frac{\sum_{i=0}^np_nq_n}{\sqrt{\sum_{i=0}^np^2}\sqrt{\sum_{i=0}^nq^2}}$$
In [16]:
# scipyのインポート
import scipy.spatial.distance as dis
# コサイン類似度
dis.cosine(X_a[2],X_a[3])
Out[16]:
0
In [17]:
# すべての文のコサイン類似度
X_cos = []
for i in X_a:
x = []
for j in X_a:
x.append(dis.cosine(i,j))
X_cos.append(x)
X_cos
Out[17]:
[[0, 0.33333333333333326, 0.42264973081037416, 0.42264973081037416], [0.33333333333333326, 0, 0.1339745962155614, 0.1339745962155614], [0.42264973081037416, 0.1339745962155614, 0, 0], [0.42264973081037416, 0.1339745962155614, 0, 0]]
In [18]:
# データフレームにしてみた。
df3 = pd.DataFrame({"a":X_cos[0],"b":X_cos[1],"c":X_cos[2],"d":X_cos[3]},index=["a","b","c","d"])
df3
Out[18]:
| a | b | c | d | |
|---|---|---|---|---|
| a | 0.00 | 0.33 | 0.42 | 0.42 |
| b | 0.33 | 0.00 | 0.13 | 0.13 |
| c | 0.42 | 0.13 | 0.00 | 0.00 |
| d | 0.42 | 0.13 | 0.00 | 0.00 |
練習問題¶
- 日本人英語学習者が以下の問題に回答しました。
When you want to break into a conversation and add something, what would you say?
- 評定者によって1 (Good)と採点されたデータは、../DATA02/TALL06_1.txtに、0 (Poor)と採点されたデータは../DATA02/TALL06_0.txtに保存されています。
- 以下の発話はGoodとPoorのどちらと判定されるべきでしょうか。
- ユークリッド距離あるいはコサイン類似度を算出してみましょう。
- can i join your conversation
- join me a conversation
- let me talk
- please listen to me