教育データ分析入門1（第2回）1

  • 2.1 分散の復習
  • 2.2 for文（個々のデータに同じ処理をする）
    • 2.2.1 for文の練習
  • 2.3 標準化と標準得点
  • 2.4 共分散と相関係数
    • 2.4.1 関係の強さを表す指標
    • 2.4.2 相関係数
  • 練習問題
  • 利用するライブラリ
In [1]:
import numpy as np

2.1 分散の復習¶

  • $\sum$（シグマ、和記号)は「全部足す」という意味。
  • $ \sum_{i=0}^n x_i^2$を
  • データ: [12,25,32,65,44,89,35]
  • でやってみると
  • $ \sum_{i=0}^n x_i^2 = 12^2 + 25^2 + 32^2 + ... 35^2$
  • データ群がどの程度散らばっているかという指標
  • 平均値から個々の値がどのれぐらい離れているかの平均値
  • だけど、個々の値から平均値を引いた値の平均は０になる
  • なので、「個々の値から平均値を引いた値」を2乗して平均する

つまり

$$ \frac{1}{n}\sum_{i=0}^n (x_i - \overline{x})^2 $$

$$ \sum_{i=0}^n x_i^2 = 12^2 + 25^2 + 32^2 + ... 35^2$$

  • 個々のデータに同じ処理をしている。

2.2 for文（個々のデータに同じ処理をする）¶

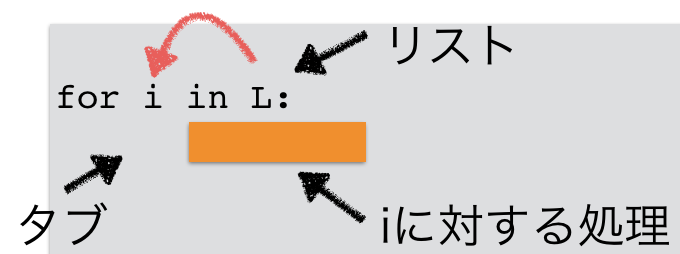
IEDA02_1.png

2.2.1 for文の練習¶

In [2]:
# Lにはデータが格納されている
L = [54,55,92,63,28]

ave = sum(L)/len(L)

# 個々のデータが平均値からどれだけ離れているか？

for i in L:
    print(i - ave)

-4.399999999999999
-3.3999999999999986
33.6
4.600000000000001
-30.4
  • これ（偏差）の平均はゼロになる（e-15は$10^{-15}$の意味。1e-1は$1\times10^{-1}=0.1$）
In [3]:
D = []

for i in L:
    D.append(i - ave)
    
sum(D)/len(D)
Out[3]:
1.4210854715202005e-15

以下のコードは$ \sum_{i=0}^n x_i^2$と同じ意味

In [4]:
# Lのデータを２乗してMに保存

L = [54,55,92,63,28]

# 空のリストを作成
M = []

for i in L:
    a = i**2
    M.append(a)

sum(M)
Out[4]:
19158
  • a += iはa + iの結果をaに代入するという意味。
In [5]:
L = [54,55,92,63,28]
a = 0
for i in L:
    a += i**2
a
Out[5]:
19158

それではfor文を使ってLの分散を求めてみましょう。

$$ \frac{1}{n}\sum_{i=0}^n (x_i - \overline{x})^2 $$

L = [56,57,92,73,65,24,37,91,79,99,100]

In [6]:
L = [56,57,92,73,65,24,37,91,79,99,100]

L_ave = sum(L)/len(L)

M = []

for i in L:
    M.append((i - L_ave)**2)

sum(M)/len(M)
Out[6]:
577.2892561983471
  • numpyで確認
In [7]:
np.var(L)
Out[7]:
577.2892561983471
  • 分散は個々のデータと平均との差を2乗しているので、その平方根が実際の「個々のデータの平均からのばらつきの平均」となる。
  • 分散の平方根を標準偏差と呼ぶ。

$$ \sqrt{\frac{1}{n}\sum_{i=0}^n (x_i - \overline{x})^2} $$

In [8]:
# このセルは描画に必要なデータを生成してるだけなので無視してください。
import matplotlib.pyplot as plt
from scipy.stats import norm
import math
%matplotlib inline

mu1 = 50
variance1 = 250
sigma1 = math.sqrt(variance1)
x1 = np.linspace(0, 100, 100)

L1 =[]
for i in norm.pdf(x1,mu1,sigma1):
    a = i * 1000
    L1.append(a)
    
mu2 = 80
variance2 = 200
sigma2 = math.sqrt(variance2)
x2 = np.linspace(0, 100, 100)

L2 =[]
for i in norm.pdf(x2,mu2,sigma2):
    a = i * 1000
    L2.append(a)

2.3 標準化と標準得点¶

  • 標準化とは集団において個々のデータの位置を示すことです。
  • 平均値や標準偏差が異なる2のテストでは同じ点数でも集団における位置が違います。

なぜ標準化するか

  • 例えば、青のテストで60点とオレンジのテストで60点は意味が違う
In [9]:
plt.plot(x1,L1)
plt.plot(x2,L2)
Out[9]:
[<matplotlib.lines.Line2D at 0x123b645e0>]
No description has been provided for this image
  • 標準得点 = (平均値 - 個々のデータ) / 標準偏差
  • 標準得点は、平均が0と分散が1になる。
  • 偏差値 = 10 * (平均値 - 個々のデータ) / 標準偏差 + 50
  • 正規分布っぽくなるので、偏差値が60以上(40以下）は全体の15%、
  • 70以上(30以下)は全体の2%ぐらいになるはず。
  • 知能指数も偏差値
  • 「なぜ平均が0になるか」ではなく、平均が0になるように操作した。

$$ \overline{z} = \frac{z_1 + z_2 + ... z_n}{n}$$

$$ = \frac{\frac{x_1 - \overline{x}}{s}+\frac{x_2 - \overline{x}}{s}+ ... + \frac{x_n - \overline{x}}{s}}{n}$$

$$ = \frac{(x_1 - \overline{x}) + (x_2 - \overline{x}) + ... + (x_n - \overline{x})}{ns}$$

$$ = \frac{(x_1 + x_2 + ... + x_n) - n\overline{x}}{ns}$$

$$ = \frac{n\overline{x} - n\overline{x}}{ns}$$

$$ = 0 $$

  • 「なぜ標準偏差（分散）が1になるか」ではなく、標準偏差が1になるように操作した。
  • 以下、$z$の標準偏差を$s_z$とする。

$$ s_z = \sqrt{\frac{(z_1 - 0)^2 +(z_2 - 0)^2 +(z_n - 0)^2 }{n}}$$

$$ = \sqrt{\frac{(\frac{x_1 - \overline{x}}{s})^2+(\frac{x_2 - \overline{x}}{s})^2+(\frac{x_n - \overline{x}}{s})^2}{n}} $$

$$ = \sqrt{\frac{(x_1 - \overline{x})^2 + (x_2 - \overline{x})^2 + (x_n - \overline{x})^2}{ns^2}} $$

$$ = \sqrt{\frac{s^2}{s^2}} $$

$$ = 1$$

  • 以下の2つのテストでそれぞれの受験者の標準得点、偏差値を求めてみましょう。

X: [48,60,29,80,77]

Y: [60,60,52,91,80]

In [10]:
X = [48,60,29,80,77]

x_m = np.average(X)
x_std = np.std(X)

X_T = []
for i in X:
    X_T.append((i-x_m)/x_std)

X_T
Out[10]:
[-0.5713086317569043,
 0.06347873686187842,
 -1.576388632069977,
 1.1214576845598496,
 0.9627608424051539]
In [11]:
X = [48,60,29,80,77]

x_m = np.average(X)
x_std = np.std(X)

X_z = (X - x_m)/x_std

X_z
Out[11]:
array([-0.57130863,  0.06347874, -1.57638863,  1.12145768,  0.96276084])
In [12]:
X = [48,60,29,80,77]

x_m = np.average(X)
x_std = np.std(X)

X_T = []
for i in X:
    X_T.append(round(10 * ((i-x_m)/x_std) + 50,0))

X_T
Out[12]:
[44.0, 51.0, 34.0, 61.0, 60.0]
In [13]:
X = [48,60,29,80,77]

x_m = np.average(X)
x_std = np.std(X)

X_T = 10*((X - x_m)/x_std)+50

X_T
Out[13]:
array([44.28691368, 50.63478737, 34.23611368, 61.21457685, 59.62760842])
  • テストYの標準得点、偏差値も同様に求めてみよう。

2.4 共分散と相関係数¶

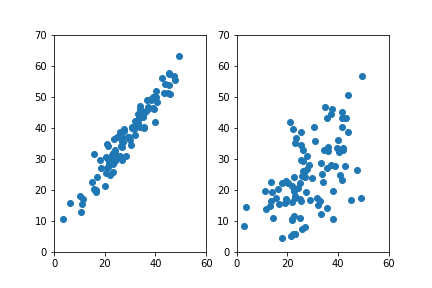
  • 以下の2つのグラフだと、右図の方が左図に比べて2つの値の関係が弱そう。
  • 右図では一方の値でもう一方の値を予測するのが難しそう。 IEDA02_2.png

2.4.1 関係の強さを表す指標¶

  • 共分散: 対応するデータの関係を表す値

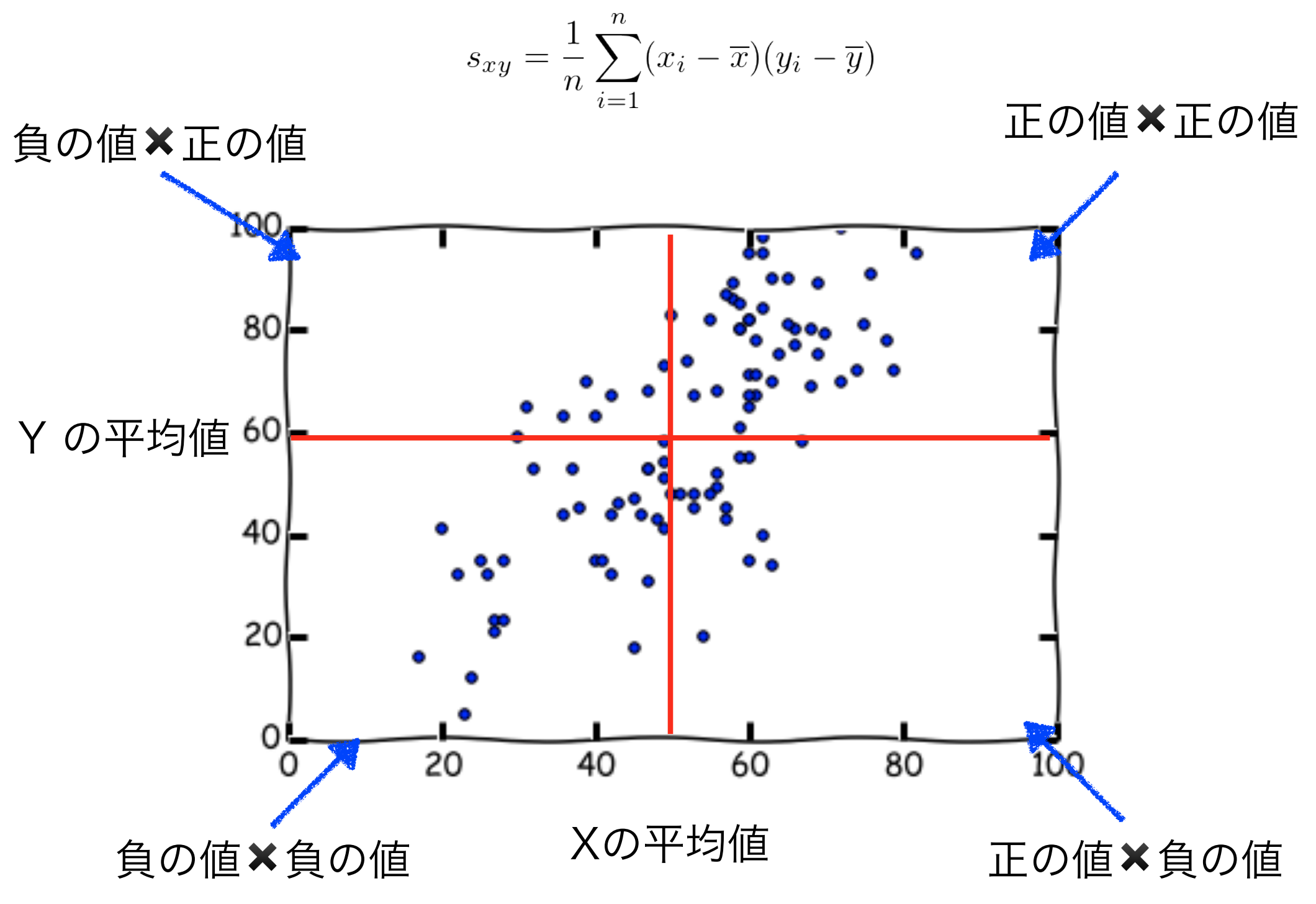
IEDA02_3.png

X = [48,60,29,80,77]

Y = [60,60,52,91,80]

Xの平均: 59

Yの平均: 69

共分散 = ((48 - 59) * (60 - 69) + (60 - 59) * ... (77 - 59) * (80 - 69)) /5

= 252

zip関数

  • 主にfor文で用いる、2つ以上のリストを同時に処理する場合に用いる。
In [14]:
A = ["み","り","バ"]
B = ["か","ん","ナ"]
C = ["ん","ご","ナ"]

for i,j,k in zip(A,B,C):
    print(i,j,k)

み か ん
り ん ご
バ ナ ナ
In [15]:
X = [48,60,29,80,77]
Y = [60,60,52,91,80]
x_m = np.average(X)
y_m = np.average(Y)
a = 0
for i,j in zip(X,Y):
    a += (i-x_m) * (j - y_m)

a / len(X)
Out[15]:
251.92

2.4.2 相関係数¶

  • 相関係数　= 共分散 /sqrt(Xの分散 * Yの分散)
  • -1から+1までの値をとる
  • マイナスは負の相関（一方の値が増えるともう一方の値が減る関係）
  • プラスは正の相関（一方の値が増えるともう一方の値が増える関係）
  • 0は無相関（2変数間に関係がない）
  • 値の絶対値が関係の強さを表す

以下のグラフだと左が0.9で右が0.6ぐらい IEDA02_2.png

  • 相関係数を求めてみよう。
In [16]:
X = [48,60,29,80,77]
Y = [60,60,52,91,80]

x_m = np.average(X)
y_m = np.average(Y)

a = 0

for i,j in zip(X,Y):
    a += (i-x_m) * (j - y_m)

cov = a / len(X)

b = 0

for i in X:
    b += (i - x_m)**2
    
x_var = b / len(X)

c = 0

for i in Y:
    c += (i - y_m)**2
    
y_var = c / len(Y)

cov /(x_var*y_var)**0.5
Out[16]:
0.917333574026356
  • numpyで確認
In [17]:
np.corrcoef(X,Y)
Out[17]:
array([[1.        , 0.91733357],
       [0.91733357, 1.        ]])

練習問題¶

X = [10,15,22,34,33,49,50,50,51,59,69]

Y = [15,22,40,39,30,61,55,48,70,81,60]

問題１

X、Yそれぞれで標準得点、偏差値を求めよ。

問題2

X、Yそれぞれの分散とXとYの共に分散を求めよ。

問題3

X,Yの相関係数を求めよ。