df.plot(kind="hist",ec="white",y="data1")
<Axes: ylabel='Frequency'>
これまでどのような試験を受けてきましたか。最初に思いつくのは入学試験や検定試験でしょうか。それから、学校の定期試験、学校の授業内で行う小テストなども思いつかれることでしょう。このような試験にはそれぞれ異なる目的があります。例えば、入学試験や検定試験は、受検者の能力の有無を見定め、合否を判定することが目的となります。高校の定期試験はどうでしょうか。高校の試験の場合、その点数は、進級することができるかどうかという合否判断の根拠、さらには、当該科目を受講した生徒が授業内容をどれぐらい理解したかという診断的情報(教師はテストの出来具合によって教え方、教える順番などを考え直します)となります。
このように、テストは何らかの目的を持って受験者の能力を測るツールです。このツールが備えてなければならない機能は何でしょうか。それは、妥当性と信頼性です。
テストを実施する人が測りたい能力を測れなければなりません。これを「妥当性」と呼びます。例えば、TOEICやTOEFLなど英語の能力に関するテストで、アジアの都市の位置を問う問題が出題されたとします。アジアの白地図が与えられ、あなたがシンガポールの位置だと思う場所をタップして解答するというような問題です。英語の能力が何かという問題を考えなければなりませんが、一般的に言って、英語が書ける、話せる、英語の単語をたくさん知っているかどうかとアジアのある都市に関する正確な位置情報を持っていることは関係があるかもしれません(アジアの都市の位置を正確に把握している人は英単語をたくさん知っているかもしれません)が、英語の能力とこのような地理に関する知識は異なるものとして捉えるべきでしょう。アジアの都市の位置をあまり正確に把握していない人でも英語が話せたり、書けたりすることは十分にあり得ることです。ここで問題としていることが妥当性です。英語のテストには英語の能力と関係する問題のみが含まれるべきであって、そうでないものは排除されるべきです。この「妥当性」を保証するためにどのようなことができるでしょうか。
次は信頼性です。信頼性とは、複数回行っても結果が(ほぼ)同じであるという性質のことを指します。あなたがもし、今朝家でご自身の身長を測ってきたとして、この授業が終わって家に帰ったときにもう一度身長を測るとします。その時に朝測った身長と夕方測った身長はほとんど同じ(1 cmも変わらない)でしょう。その場合、あなたが持っている身長計の信頼性は高いと言えます。これを試験の文脈に置き換えることは簡単ではありませんが、単純化すると、あなたが今日TOEICを受験して得たスコアと明日受験して得るスコアが大きくは変わっていないかということが試験における信頼性です。
ここで、構成概念という心理学用語を導入します。性格、能力、不安や緊張と言った心理的状態は、目に見えたり手で触れたりすることができません。だからと言ってこれらが「存在しない」というのはかなり乱暴な考えです。英語が上手に書ける人とそうではない人がいて、何らかの英語の試験をするとそれなりに点数の差があるものです。そのため、目に見えることはありませんが、「英語力」という構成概念を仮定して、英語の試験は何らかの英語力を測定していると考えます。例えば、英語力がそんなに高くない人でも正答できる問題から英語力がかなり高くないと正当できない問題まで複数の問題を提示し、それらを採点することで英語力を測定していると考えます。しかしながら、一般に我々が知りたい英語力とは英語の問題に正答できるかどうかではなく、実際的な場面で英語を読んだり、聞いたり、話したり、書いたりする能力です。なので、英語の試験は英語力を直接的ではなく、間接的に測っているということになります。構成概念という目に見えないものを仮定し、さらにそれを間接的に測定しているので、テストにはそれほど高い精度を求めることはできません。また、英語の試験の得点がゼロであっても英語力がまったくないと言い切れるわけではありません。重さが0グラムのものに重さはありませんが、英語の試験ではそうではありません。
構成概念を前提とした能力の間接的な測定はあまり正確なものではありませんが、テストは受験者の人生に大きな影響を与える場合があります。だから、そのために、テストの信頼性、妥当性を検討し、より品質の高いテストを作成することが重要なのです。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
d = np.random.normal(50,10,100)
e = np.random.normal(50,20,100)
df = pd.DataFrame({"data1":d,"data2":e})
df.plot(kind="hist",ec="white",y="data1")
<Axes: ylabel='Frequency'>
同じ平均値でも違う分布
df.hist(ec="black")
array([[<Axes: title={'center': 'data1'}>,
<Axes: title={'center': 'data2'}>]], dtype=object)
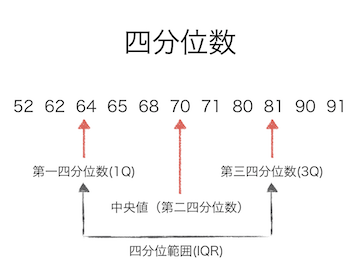
記号の復習
$\sum$(シグマ、和記号)は単なるの和。
$ \sum_{i=0}^n x_i^2$を
データ: [12,25,32,65,44,89,35]
でやってみると
$ \sum_{i=0}^n x_i^2 = 12^2 + 25^2 + 32^2 + ... 35^2$
分散とは
f = np.random.normal(50,5,100)
g = np.random.normal(50,30,100)
df2 = pd.DataFrame({"data1":d,"data2":e})
つまり
$$ Var = \frac{1}{n}\sum_{i=0}^n (x_i - \overline{x})^2 $$以下の2つの群(水色とオレンジ)は平均が50で分散が異なる。
df2.plot(kind="hist",alpha=0.5,ec="black")
<Axes: ylabel='Frequency'>
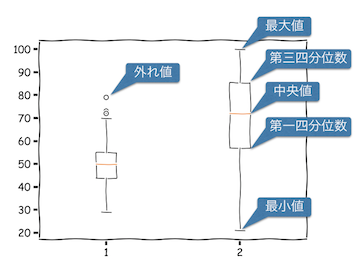
| 用語 | 意味 |
|---|---|
| 最小値 | データの中で最も小さい値 |
| 最大値 | データの中で最も大きい値 |
| 第一四分位数 | データを小さい方から並べて小さい方から25%のところ |
| 中央値 | データを小さい方から並べて小さい方から50%のところ |
| 第三四分位数 | データを小さい方から並べて小さい方から75%のところ |
| 四分位範囲 | 第一四分位数 - 第三四分位数 |
| 外れ値 (大きい方) | 第三四分位数 + 1.5×四分位範囲より大きい値 |
| 外れ値 (小さい方) | 第一四分位数 - 1.5×四分位範囲より小さい値 |
外れ値
箱ひげ図