教育データ分析入門2（第5回）

  • 5.1 統計的検定
    • 5.1.1 母分散が既知の場合
    • 5.1.2 母分散が未知な場合
In [2]:
# 使用するパッケージ
import pandas as pd
import numpy as np
from scipy.stats import t,scoreatpercentile,norm
import matplotlib.pyplot as plt
%matplotlib inline

5.1 統計的検定¶

5.1.1 母分散が既知の場合¶

  • 母集団に関する仮説を標本から得た情報に基づき判断すること。

問4: あるプログラムの受講後のテストの結果を用いて、その効果を測定する。過去のテストの結果は、平均$\mu = 150$、分散$\sigma^2 = 64$である。新たな受講生30人に対し同じテストを行ったところ標本平均$\bar{x} = 145$であった。標本集団に対してもこのプログラムはこれまで同様機能しているか（標本集団は過去に受験した集団と同じだと言えるか）。

  • 帰無仮説と対立仮説を設定する。

    • 帰無仮説($H_0$): $\mu = 150$ (標本集団にはこれまでと同様の効果があった)
    • 対立仮説($H_1$): $\mu < 150$ (標本集団をこれまでの集団に含めると$\mu = 150$ではない)

  • $H_0$を認めた場合に標本集団が得られる確率を設定する（ここでは5%）。

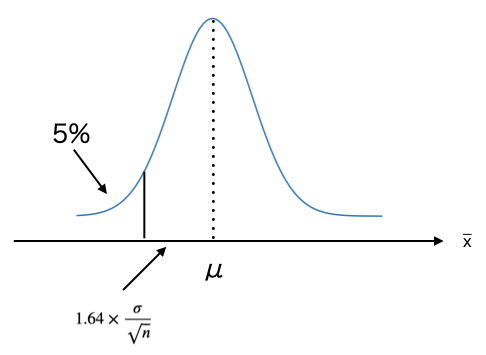
  • これを棄却域（有意水準）と言い、標本平均が棄却域にある場合、$H_0$を棄却し、$H_1$を採択する。 fig01

  • これまでの1000人のテストの結果を母集団とする。

  • この母集団から標本を抽出し、$\bar{x} = 145$となる確率を考える。

  • 母平均$\mu = 150$、母分散$\frac{\sigma^2}{\sqrt{n}} = \frac{8}{\sqrt{30}}$で、棄却域のパーセント点を5%とし、以下を計算すると、 $$\mu - 1.64 \times \frac{8}{\sqrt{30}}$$

In [3]:
150 - 1.64 * 8/ np.sqrt(30)
Out[3]:
147.60462668184408
  • 147.6点が5%点（下側5%点）となり、145はそれ以下なので、この標本平均が、母平均$\mu = 150$、母分散$\sigma^2 = 64$の母集団から得られる確率が5%以下であるため、$H_0$を棄却し、$H_1$を採択する。
  • 以下、本当にそうなるか確認してみる。
In [4]:
# 以下を母集団とみなす。
x = np.random.normal(150, 8, 1000)

L = []

for i in range(1000):
    s = np.random.choice(x,30)
    L.append(np.average(s))

n = 0

for i in L:
    if i < 147.60:
        n +=1
        
n/1000
Out[4]:
0.048
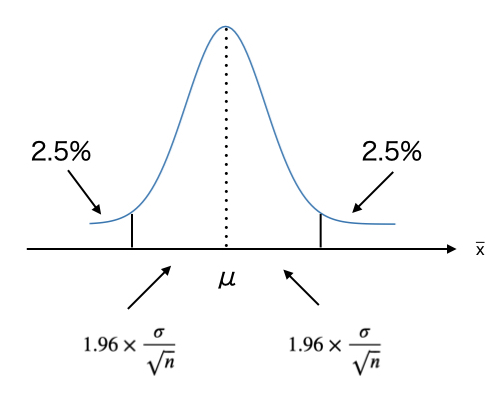
  • 問4の対立仮説$(H_1)$は$\mu < 150$であったが対立仮説$(H_1)$が$\mu \neq 150$の場合は以下のように上側確率を設定し、棄却域を5%にすると、上側、下側のパーセント点が2.5%となる。 fig02

5.1.2 母分散が未知な場合¶

  • 問5: 東京都にある公立高校3年生のあるテストの2015年の平均点は120点だった。近年の教育実践を考慮すると、平均点は上昇していると考えることができる。それを証明するために同じ条件の高校3年生30人に同じテストを受験させた。平均値は127点で、不偏分散は25.5であった。「平均点は上昇している」と主張することはできるか。このテストの点数は正規分布に従うと仮定し、有意水準5%で検定せよ。

  • 整理すると、$ \mu = 120, n = 30, \bar{x} = 127, U^2 = 25.5$。

  • $H_0: \mu = 120, H_1 > 120$

  • 以下の$T$が自由度$n - 1$のt分布に従う。

$$ T = \frac{\bar{x} - \mu}{\frac{U}{\sqrt{n}}}$$

$$ T = \frac{127 - 120}{\frac{5.04}{\sqrt{30}}}$$

$$ = 7.60 $$

In [6]:
t.ppf(0.95,30)
Out[6]:
1.6972608943617378
  • t分布の上側5%点が1.69で、7.60はそれを超えているので、$H_0: \mu = 120$は棄却され、 $H_1 > 120$が採択される。
  • これを「有意水準5%で統計的に差がある（上昇している）」と言う。