In [1]:
# 使用するパッケージ
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import scipy
from scipy import integrate
import seaborn as sns
3.1 正規分布¶
- 正規分布は統計学で頻繁に出てくる確率分布のひとつです。
- ここでは、確率分布とは何か、正規分布とは何か、正規分布をどのように利用するかを理解します。
- 統計的推定・検定の考え方を理解します。
3.1.1 前提¶
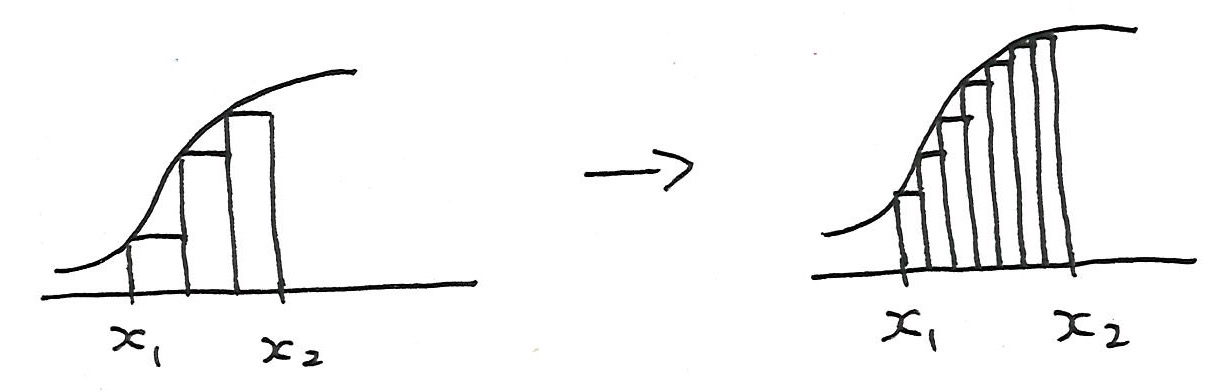
- 以下の図で曲線と直線の間の面積を求めるとき、以下のように対象を長方形に区切って面積を求めることを区分求積法と言います。
- 区分求積法では長方形の幅を小さくする（対象の分割数を大きくする）と実際の面積に近くなります。
- 以下は$y = x^2$のグラフである。
In [2]:
x = np.arange(-10,10,0.1)
y = x**2
plt.ylim([0,100])
plt.plot(x,y)
Out[2]:
[<matplotlib.lines.Line2D at 0x12fa6bfa0>]
- このグラフで$y = x^2$と$y = 0$に挟まれたところで$x$が0から10までの面積を求める。
In [4]:
# 関数の定義
def func(x):
return x**2
In [5]:
# 下限値
a = 0
# 上限値
b = 10
# 分割数
n = 10000
#長方形の幅
dx = (b-a)/n
In [10]:
s = 0
for i in range(1,n):
x1 = dx*i
f1 = func(x1)
s += dx*f1
s
Out[10]:
333.28333499999957
- このような面積は積分で求めることが可能である。
- 微分すると$x^2$になる関数は$F(x) = \frac{1}{3}x^3$なので計算で以下のように求めることが可能である。
$$ \int_{0}^{10} x^2dx\\ = \frac{1}{3}10^3 - \frac{1}{3}0^3\\ = \frac{1000}{3}\\ = 333.3333.... $$
- 以下はscipyを用いて計算する方法である。
In [6]:
ans,err = integrate.quad(func,a,b)
ans
Out[6]:
333.33333333333337
3.1.2 ヒストグラムと正規分布¶
ヒストグラムとは、以下のようにx軸を階級、y軸を頻度としたグラフである。
ひとつの階級の面積の全体に対する割合はその階級にあるデータ数の全体に対する割合と同じである。
全体の面積を1とした場合、それぞれの階級の面積は全体に対する割合として扱うことができる。
この割合を確率と考える（雑に言うと、過去のことが割合、未来のことが確率）。
- 2016年から2025年までにこのクラスを履修した4年生以上の割合は9%。
- 2025年にこのクラスを履修している学生を1人選んだ時にその学生が4年生以上の確率は9%
たとえば、以下のデータは、あるテストの点数を標準化したものであるとした場合、新たな受験者がこのテストを受験してある区間のスコアをとる確率は、その区間のヒストグラムの面積の全体に対する割合である。
このように考えると、ヒストグラムは、確率の散らばり具合を示しているので、確率分布と捉えることができる（分布とは散らばり具合のこと）。
In [7]:
np.random.seed(365)
x = np.random.standard_normal(1000)
ax = sns.histplot(x, kde=False, stat='density', label='samples',bins=30)
- データを収集するとさまざまな場面で、平均値付近のデータが多く、平均値から離れていくと徐々にデータの数が減っていく左右対称な分布となることが多い。
- このヒストグラムで表された分布を１本の線で表す。
- これが正規分布である。正規分布は以下の確率密度関数で与えられる確率分布である（赤い線）。
$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} exp(-\frac{(x - \mu)^2}{2\sigma^2})$$
- $exp$はネイピア数。2.7ぐらい。$\pi$と似たようなものと考えてくれればOK。
In [8]:
np.random.seed(365)
x = np.random.standard_normal(1000)
ax = sns.histplot(x, kde=False, stat='density', label='samples',bins=30)
x0, x1 = ax.get_xlim()
x_pdf = np.linspace(x0, x1, 100)
y_pdf = scipy.stats.norm.pdf(x_pdf)
ax.plot(x_pdf, y_pdf, 'r', lw=2, label='pdf')
Out[8]:
[<matplotlib.lines.Line2D at 0x12fcb1190>]
- ここで示した正規分布は、平均が0で分散（標準偏差）が1の正規分布で、これを特別に標準正規分布と呼ぶ。
- 標準正規分布の性質は数学的によく知られていて、また、多くのデータが正規分布に従うとされている。
- そのため、データの母集団が正規分布であると仮定して、分析を行う場合が多い。
- 正規分布には以下のような特徴がある。
- 左右対称
- 平均が１番多い
- $\sigma$が分布の広がりを示す。
3.2.2 点推定¶
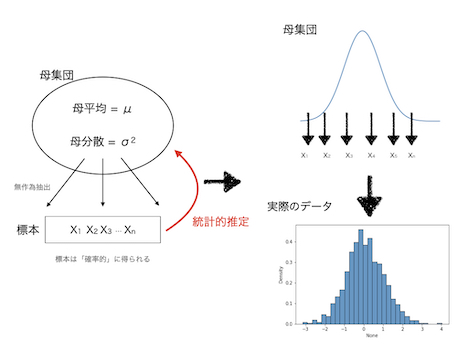
- 一般に、母平均、母分散の推定値には、標本平均、不偏分散を使用する。
- 母集団の平均値である母平均がどれぐらいかを推定する値として標本平均を用いる。
- 推定値はサンプル数(n)が大きくなれば母数に近づく。
- 点推定では、母平均の推定値として標本平均、母分散として不偏分散を用いる。
- 標本分散: $$S^2 = \frac{(X_1 - \bar{X})^2 + (X_2 - \bar{X})^2 + ... (X_n - \bar{X})^2}{n} $$
- 不偏分散 $$U^2 = \frac{(X_1 - \bar{X})^2 + (X_2 - \bar{X})^2 + ... (X_n - \bar{X})^2}{n - 1} $$
- 標本分散は母分散を小さく見積もってしまうので、$n$ではなく$n-1$で割る。
不偏分散の分母が$n - 1$の理由
- 標本分散を求める際に使っている平均は母平均ではなく標本平均なので、標本平均は母平均より標本集団のそれぞれのデータに近い。そのため、標本分散は母分散を実際の値より小さく見積もっている。
- ここで、本当は神様しか知らない正規分布に従う母集団を設定して、点推定の精度を確認してみます。
- numpyを用いて平均が100、標準偏差が10(分散が100)の母集団からランダムに1000000個のデータを生成します。
- このデータから標本を抽出し、標本数を増加させ、その標本分散、不偏分散、平均値の変化を観察します。
In [9]:
x = np.random.normal(100, 10, 1000000)
In [10]:
U = []
for i in range(50,50000,100):
s = np.random.choice(x,i)
U.append(np.var(s))
In [11]:
n = list(range(50,50000,100))
plt.plot(n,U)
Out[11]:
[<matplotlib.lines.Line2D at 0x12fa7e760>]
In [12]:
S = []
for i in range(50,50000,100):
s = np.random.choice(x,i)
S.append(np.var(s,ddof=1))
In [13]:
plt.plot(n,S)
Out[13]:
[<matplotlib.lines.Line2D at 0x12fdbeaf0>]
In [14]:
def var2(X):
m = np.average(X)
s = 0
for i in X:
s += (i - m)**2
return s / (len(X) - 2)
In [15]:
U2 = []
for i in range(50,50000,100):
s = np.random.choice(x,i)
U2.append(var2(s))
In [16]:
plt.plot(n,U2)
Out[16]:
[<matplotlib.lines.Line2D at 0x12fe40b50>]
In [17]:
M = []
for i in range(50,50000,100):
m = np.random.choice(x,i)
M.append(np.average(s))
In [18]:
plt.plot(n,M)
Out[18]:
[<matplotlib.lines.Line2D at 0x12fece520>]
3.2.3 区間推定（分散が既知）¶
- 母集団から標本を抽出して、「XXは○○%の確率でYYの範囲に含まれる」などと主張したい。
- 例: 「あるテストの東京都の高校生の平均点は95%の確率で82点から83点の間に含まれる」
- このような主張をする理由としては、過去との比較や異なる母集団同士の比較などが考えられる。
問1: ある正規分布に従う母集団（$\mu$が未知、$\sigma^2=25$)からひとりの生徒の点数を取り出したとき、その点数が65点だった。信頼度95%で母集団の平均を推定せよ。
- 母集団は正規分布に従っているので、以下のようなことが既に分かっている。
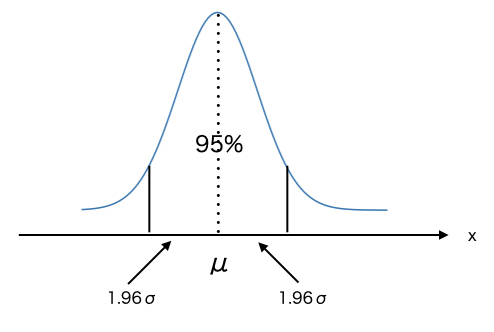
- $\mu$から左右に$1.96\sigma$離れたところの面積が全体の95%である。
- 95%の確率で以下の式が成り立つ。
$$ \mu -1.96\sigma \leq x \leq \mu +1.96\sigma$$
- この式を$\mu$に関して整理すると
$$ x -1.96\sigma \leq \mu \leq x +1.96\sigma$$
- となり、母集団の平均$\mu$は95%の確率で
$$ 65 - 1.96 \times 5 \leq \mu \leq 65 + 1.96 \times 5$$
- これを計算すると
$$ 55.2 \leq \mu \leq 74.8 $$
- となり、上の式は95%で成り立つので、「母集団の平均値は95%の確率で55.2から74.8の間に含まれる」と主張できる。
注: 95%の信頼区間とは、このサンプリングを100回行った場合、その95回で算出した信頼区間に母集団の平均が含まれるという意味である。
- それでは、$\mu -1.96\sigma \leq x \leq \mu +1.96\sigma$実際に95%の確率で成り立つか確かめてみましょう。
- 以下では、平均50、標準偏差5のデータをランダムに生成し、その中からひとつのデータをランダムに取り出し、そのデータ($x$)において$\mu -1.96\sigma \leq x \leq \mu +1.96\sigma$が成り立つか確認しています。
In [19]:
X = np.random.normal(50, 5, 100000)
n = 0
for i in range(1000):
x = np.random.choice(X)
lower = x - 1.96 * 5
upper = x + 1.96 * 5
if lower <= 50 and 50 <= upper:
n += 1
n/1000
Out[19]:
0.959
練習問題¶
正規分布に従う母集団（$\mu$が未知、$\sigma^2=200$)からひとりの生徒の点数を取り出したとき、その点数が120点だった。信頼度95%で母集団の平均を推定せよ。